Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Faltungsformel

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Verifiziere die Faltungsformel $ \mbox{${\operatorname{\mathcal{L}}}(f\ast g) = {\operatorname{\mathcal{L}}}(f)\cdot{\operatorname{\mathcal{L}}}(g)$}$.

Verwende die Faltungsformel zur Berechnung von $ \mbox{$\int_0^1 \exp(1-u)\cdot u \, du$}$. Berechne zur Probe direkt.

Mit Hilfe der Substitution $ \mbox{$t=v-u$}$ folgt die Faltungsformel

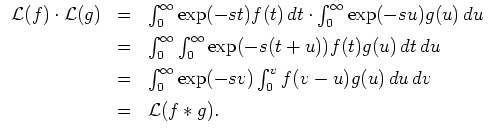
$ \mbox{$\displaystyle \begin{array}{rcl} {\operatorname{\mathcal{L}}}(f)\cdot... ...\,dv\vspace*{2mm}\\ &=&{\operatorname{\mathcal{L}}}(f \ast g). \end{array}$}$

Sei $ \mbox{$f(t) = \exp(t)$}$, sei $ \mbox{$g(t) = t$}$, und sei $ \mbox{$h = f\ast g$}$. Zu berechnen ist $ \mbox{$h(1)$}$.

Es wird

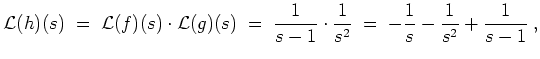
$ \mbox{$\displaystyle {\operatorname{\mathcal{L}}}(h)(s) \; =\; {\operatorname... ...1}\cdot\frac{1}{s^2} \; =\; -\frac{1}{s} - \frac{1}{s^2} + \frac{1}{s-1}\; , $}$
was rücktransformiert
$ \mbox{$\displaystyle h(t)\; =\; -1 - t - \exp(t) $}$
liefert, und also $ \mbox{$h(1) = \exp(1) - 2$}$.

Direkt wird

$ \mbox{$\displaystyle \int_0^1 \exp(1-u)\cdot u \, du\; =\; [-\exp(1-u)\cdot u]_0^1 +\int_0^1 \exp(1-u)\, du \;= \; -1 + [-\exp(1-u)]_0^1\; =\; e - 2\; . $}$
(Autoren: Künzer/Meister/Nebe)

siehe auch:

  automatisch erstellt am 25.  1. 2006