Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Trapezregel bei Bessel-Funktionen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Die Bessel-Funktionen $ \mathcal{J}_k$ besitzen für ganzzahliges $ k$ die Integraldarstellung

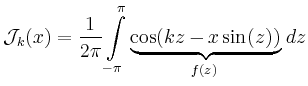
$\displaystyle \mathcal{J}_k(x) = \frac{1}{2\pi} \int\limits_{-\pi}^{\pi} \underbrace{\cos(kz-x\sin(z))}_{f(z)}\,dz $

und sind für $ k = 0,\ldots ,4$ in der folgenden Abbildung dargestellt.

\includegraphics[width=0.5\linewidth]{Trapezregel_Bessel.eps}

Bei der Berechnung mit der Trapez-Regel nutzt man aus, dass

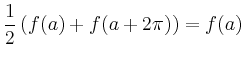
$\displaystyle \frac{1}{2}\left(f(a)+f(a+2\pi)\right) = f(a) $

und dass $ f$ gerade ist. Wählt man die Punkte

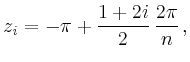
$\displaystyle z_{\mathit i} = -\pi+\frac{1+2i}{2}\, \frac{2\pi}{n}\,, $

so ist die Summe

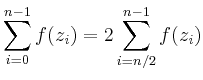
$\displaystyle \sum\limits_{i=0}^{n-1} f(z_{\mathit i}) = 2\sum\limits_{i=n/2}^{n-1} f(z_{\mathit i}) $

zu bilden.

Wie die Folge der Approximationen von $ \mathcal{J}_1(2)$ mit $ n=4,8, \ldots 64$ Punkten zeigt, ist die Konvergenz äußerst schnell.

\begin{tabular}{r\vert l} $n$\ & \\ \hline & \\ [-1.5ex] 4 & \underline{0}.4546... ... & \\ [-1.5ex] 64 &\underline{0.57672480775687338720244824226913} \end{tabular}

Diese hohe Genauigkeit der Trapezregel ist typisch für glatte periodische Integranden und kann mit einer genaueren Darstellung des Fehlers, der Euler-Maclaurinschen Summenformel, begründet werden.

(Autoren: Höllig/Hörner)

siehe auch:

  automatisch erstellt am 12.  5. 2010