Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon:

Beispiel: Reelle Fourier-Reihe

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Es wird die reelle Fourier-Reihe der $ 2\pi$-periodischen Fortsetzung der abgebildeten Funktion bestimmt.

\includegraphics[clip,width=.9\linewidth]{b_fourier_reihe_f}

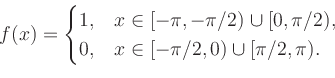
\begin{displaymath} f(x)= \begin{cases} 1, & x\in[-\pi,-\pi/2)\cup[0,\pi/2), \\ 0, & x\in[-\pi/2,0)\cup[\pi/2,\pi). \end{cases}\end{displaymath}

(i) Kosinus-Koeffizienten:

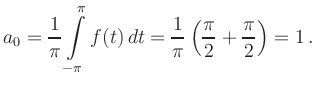
$\displaystyle a_0 = \frac{1}{\pi} \int\limits_{-\pi}^\pi f(t)\,dt = \frac{1}{\pi}\left( \frac{\pi}{2}+\frac{\pi}{2}\right) = 1 \,. $

Für $ k\ge 1$ erhält man, da der Kosinus eine gerade Funktion ist,
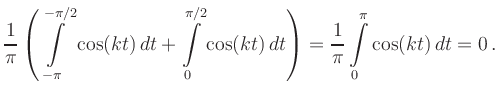$\displaystyle a_k$ $\displaystyle =$ $\displaystyle \frac{1}{\pi} \left( \int\limits_{-\pi}^{-\pi/2}\cos(kt)\,dt + \i... ...i/2}\cos(kt)\,dt \right) = \frac{1}{\pi} \int\limits_0^\pi \cos(kt)\,dt = 0 \,.$  

(ii) Sinus-Koeffizienten:

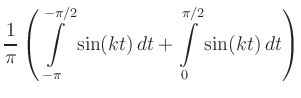$\displaystyle b_k$ $\displaystyle =$ $\displaystyle \frac{1}{\pi} \left( \int\limits_{-\pi}^{-\pi/2}\sin(kt)\,dt + \int\limits_0^{\pi/2}\sin(kt)\,dt \right)$  
  $\displaystyle =$ $\displaystyle \frac{1}{\pi} \left( \left[ -\frac{\cos(kt)}{k}\right]_{-\pi}^{-\pi/2} +\left[ -\frac{\cos(kt)}{k}\right]_0^{\pi/2} \right)$  
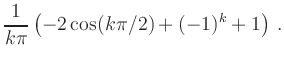  $\displaystyle =$ $\displaystyle \frac{1}{k\pi} \left(-2\cos(k\pi/2)+(-1)^k+1\right) \,.$  

Jenachdem ob $ \cos(k\pi/2)$ den Wert 0, $ 1$ oder $ -1$ hat, unterscheidet man $ 3$ Fälle:
$ k$ ungerade: $ b_k =0$,
$ k=4m$: $ b_{4m} =0$,
$ k=4m+2$: $ b_{4m+2}=4/((4m+2)\pi)$.

(iii) Fourier-Reihe von $ f$:

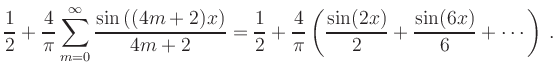
$\displaystyle \frac{1}{2}+\frac{4}{\pi}\sum_{m=0}^\infty \frac{\sin\left((4m+2... ...\frac{4}{\pi}\left(\frac{\sin(2x)}{2} + \frac{\sin(6x)}{6} + \cdots\right) \,. $

Die Abbildung zeigt die Partialsummen

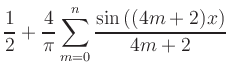
$\displaystyle \frac{1}{2} +\frac{4}{\pi}\sum\limits_{m=0}^n \frac{\sin\left((4m+2)x\right)}{4m+2} $

für $ n=2$ und $ n=8$.

\includegraphics[clip,width=.9\linewidth]{b_fourier_reihe_f_p1_p8}

Da $ f$ unstetig ist, konvergiert die Fourier-Reihe sehr langsam. Man beobachtet Überschwingungen in der Nähe der Sprungstellen, das sogenannte Gibbsche Phänomen.

siehe auch:

  automatisch erstellt am 22.  9. 2016