Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Beispiel: Residuensatz

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Als Beispiel wird die Funktion

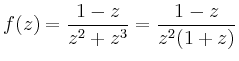
$\displaystyle f(z)=\frac{1-z}{z^2+z^3}=\frac{1-z}{z^2(1+z)} $

und für $ C$ der entgegen dem Uhrzeigersinn orientierte Kreis um 0 mit Radius $ 2$ betrachtet.

Bei $ z=0$ hat $ f$ eine Polstelle zweiter Ordnung, und für das Residuum an dieser Stelle ergibt sich

$\displaystyle \underset{0}{\operatorname{Res}}f$ $\displaystyle = \frac{1}{1!}\left[\frac{d}{dz}(z^2f(z))\right]_{z=0} =\left[\fr... ...frac{1-z}{1+z}\right)\right]_{z=0} =\left[-\frac{2}{(1+z)^2}\right]_{z=0}=-2\,.$    

Bei $ z=-1$ hat $ f$ eine einfache Polstelle, und für das Residuum an dieser Stelle erhält man


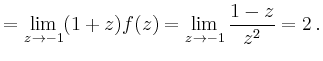$\displaystyle \underset{-1}{\operatorname{Res}}f$ $\displaystyle = \lim_{z\to -1} (1+z)f(z) = \lim_{z\to -1}\frac{1-z}{z^2}=2\,.$    

Da beide Polstellen im Inneren von $ C$ liegen, folgt mit Hilfe des Residuensatzes


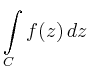$\displaystyle \int\limits_C f(z)\,dz$ $\displaystyle = 2\pi\mathrm{i}(\underset{0}{\operatorname{Res}}f +\underset{-1}{\operatorname{Res}}f) = 2\pi\mathrm{i}(-2 +2) =0\,.$    

[Verweise]
  automatisch erstellt am 21. 11. 2013