Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Erstes Integral und Phasen-DGL

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Sei $ n = 2 .$ Gegeben sei das autonome System

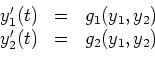
\begin{displaymath} \begin{array}{ccc} y_1'(t) & = & g_1(y_1,y_2) \\ y_2'(t) & = & g_2(y_1,y_2) \\ \end{array}\end{displaymath}

Annahme $ y_1(t)$ sei umkehrbar. Die Umkehrung sei $ t = t(y_1) .$ Dann gilt für $ y_2(t(y_1))$ nach Kettenregel und der Formel für die Ableitung der Umkehrfunktion

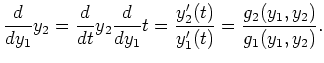
$\displaystyle \frac{d}{dy_1} y_2 = \frac{d}{dt} y_2 \frac{d}{dy_1} t = \frac{y_2'(t)}{y_1'(t)} = \frac{g_2(y_1,y_2)}{g_1(y_1,y_2)} .$

Beachte, da $ y_1(t)$ umkehrbar ist, ist $ g_1(y_1,y_2) = y_1'(t) \neq 0 .$

Die Differentialgleichung

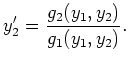
$\displaystyle y_2' = \frac{g_2(y_1,y_2)}{g_1(y_1,y_2)} .$

nennt man die Phasen - DGL des autonomen Systems.

Läßt sich die Phasen - DGL durch Separation lösen, dann erhält man über

$\displaystyle g_1(y_2) \ dy_2 = g_2(y_1) \ dy_1 $

durch Integration beider Seiten

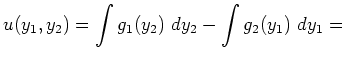$\displaystyle u(y_1,y_2) = \int g_1(y_2) \ dy_2 - \int g_2(y_1)\ dy_1 =$    const. $\displaystyle .$

Offensichtlich ist $ u(y_1,y_2)$ ein erstes Integral des Ausgangssystems.

Zur Veranschaulichung solcher Systeme und der Phasen - DGL im $ \mathbb{R}^2 $ in gewohnter Weise schreibt man oft $ x$ statt $ y_1$ bzw. $ y$ statt $ y_2 .$ Konkret:

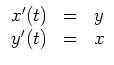
$\displaystyle \begin{array}{ccc} x'(t) & = & y \\ y'(t) & = & x \end{array}$

Dann ist $ y' = \frac{x}{y} $ die zugehörige Phasen - DGL. Aus $ y dy = x dx $ erhält man $ u(x,y) = y^2 - x^2 $ als erstes Integral.

Erste Integrale sollte man nicht mit den Lösungen des Systems verwechsln. Obiges System besitzt z.B. $ x(t) = \cosh t$ und $ y(t) = \sinh t$ als Lösungen .

Allgemein gilt: Ist $ f$ eine $ C^1$ - Funktion und $ u$ ein erstes Integral, dann ist auch $ f(u)$ ein erstes Integral. Erste Integrale sind also in keinster Weise eindeutig.

(Aus: Vorlesungsskript HM3)

siehe auch:

  automatisch erstellt am 25.  1. 2006