Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Erste Integrale und Phasen-DGL-System

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Sei nun $ n$ beliebig und

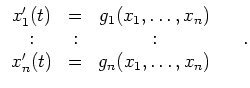
$\displaystyle \begin{array}{ccc} x_1'(t) & = & g_1(x_1, \ldots, x_n) \\ : & : & : \\ x_n'(t) & = & g_n(x_1, \ldots, x_n) \end{array} \ \ \ \ . $

Annahme $ x_n(t)$ sei umkehrbar und $ t = t(x_n)$ die Umkehrung. (Man könnte natürlich auch jedes andere $ x_i(t)$ als umkehrbar annehmen und nachfolgende Überlegungen entsprechend durchführen)

Das System

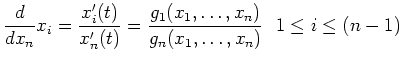
$\displaystyle \frac{d}{dx_n} x_i = \frac{x_i'(t)}{x_n'(t)} = \frac{g_1(x_1, \ldots ,x_n)} {g_n(x_1, \ldots , x_n)} \ \ 1 \leq i \leq (n-1) $

nennt man das zugehörige Phasen - DGL - System. Nach dem Existenz- und Eindeutigkeitssatz besitzt dies für beliebige Anfangsbedingungen $ x_1(x_0), \ldots , x_{n-1}(x_0) $ Lösungen. Die allgemeine Lösung des Phasen - DGL - Systems hängt somit von $ n-1$ beliebigen Integrationskonstanten $ c_1, \ldots , c_n $ ab, die wegen der Eindeutigkeit der Lösung einer Gleichung der Form

$\displaystyle c_i = u_i(x_1(x_n), \ldots, x_n) $

genügen. Setzt man $ x_n = x_n(t)$, dann sieht man, daß die Funktionen $ u_i(x_1(t), \ldots, x_n(t))$ erste Integrale des Ausgangssystems sind. Ist $ f$ eine beliebige Funktion der Klasse $ C^1,$ so ist $ f(u_1, \ldots, u_{n-1})$ ebenfalls ein erstes Integral.

Wir konkretisieren dies an folgendem autonomen System:

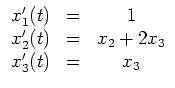
$\displaystyle \begin{array}{ccc} x_1'(t) & = & 1 \\ x_2'(t) & = & x_2 + 2 x_3 \\ x_3'(t) & = & x_3 \\ \end{array}$

Man beachte, daß nach der dritten Gleichung $ x_3(t) = k e^{t} .$ Daher ist $ x_3(t)$ invertierbar.

Als Phasen - DGL - System ergibt sich:

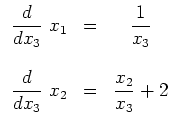
$\displaystyle \begin{array}{ccc} \displaystyle \frac{d}{dx_3} \ x_1 & = & \disp... ...style \frac{d}{dx_3} \ x_2 & = & \displaystyle \frac{x_2}{x_3} + 2 \end{array}$

$ x_1 = \ln x_3 + c_1$ löst die erste Gleichung.

Die zweite Phasen - DGL besitzt die homogene Lösung $ {x_2}_h = c \cdot x_3 .$ Variation der Konstanten ergibt den Ansatz $ {x_2}_p = c(x_3)x_3$ für eine partikuläre Lösung. Einsetzen in die DGL ergibt

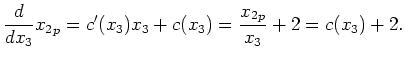
$\displaystyle \frac{d}{dx_3}{x_2}_p = c'(x_3)x_3 + c(x_3) = \frac{{x_2}_p}{x_3} + 2 = c(x_3) + 2 .$

Es folgt $ c'(x_3) = \frac{2}{x_3} $ und daher $ c(x_3) = 2 \ln x_3 .$ Die allgemeine Lösung der zweiten Gleichung ist dann

$\displaystyle x_2 = 2 x_3 \ln x_3 + x_3 c_2 .$

Somit folgt

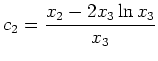
$\displaystyle c_1 = x_1 - \ln x_3$    und $\displaystyle c_2 = \frac{x_2 - 2 x_3 \ln x_3}{x_3} $

und

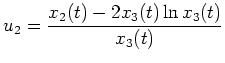
$\displaystyle u_1 = x_1(t) - \ln x_3(t)$    bzw. $\displaystyle u_2 = \frac{x_2(t) - 2 x_3(t) \ln x_3(t)}{x_3(t)} $

sind erste Integrale des gegebenen autonomen Systems.

(Aus: Vorlesungsskript HM3)
[Verweise]
  automatisch erstellt am 25.  1. 2006