Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Charakteristisches System

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Gegeben sei

$\displaystyle f_x + (y+2z)f_y + zf_z = 0 .$

Diese PDG stimmt mit ihrer reduzierten überein. Das charakteristische System lautet:

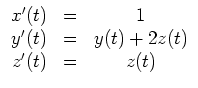
$\displaystyle \begin{array}{ccc} x'(t) & = & 1 \\ y'(t) & = & y(t) + 2z(t) \\ z'(t) & = & z(t) \end{array} $

Zur Berechnung eines ersten Integrals dieses Systems ist ein zugehöriges System von Phasen - DGL zu betrachten. Mit $ x_1 = x, x_2 = y , x_3 = z$ ist das System genau jenes, welches in Abschnitt 5.2 gerechnet wurde. Das System der Phasen - DGL ist:

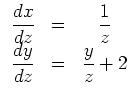
$\displaystyle \begin{array}{ccc} \displaystyle \frac{dx}{dz} & = & \displaystyl... ... \displaystyle \frac{dy}{dz} & = & \displaystyle \frac{y}{z} + 2 \end{array} $

$ x = \ln z + c_1$ ist die allgemeine Lösung der ersten Gleichung, jene der zweiten Gleichung ist $ y = 2 z \ln z + z c_2 .$

Auflösen nach den Konstanten $ c_i$ ergibt die ersten Integrale :

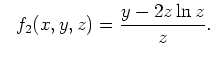
$\displaystyle f_1(x,y,z) = x - \ln z \ $    und $\displaystyle \ \ f_2(x,y,z) = \frac{y - 2 z \ln z}{z} .$

$ f_1 $ und $ f_2$ sind somit Lösungen der PDG, wie auch alle anderen ersten Integrale des charakteristischen Systems.

(Aus: Vorlesungsskript HM3)
[Verweise]
  automatisch erstellt am 25.  1. 2006