Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Charakteristisches System einer PDG mit konstanten Koeffizienten

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Wenn die Koeffizienten einer PDG konstant sind, dann ist das charakteristische System der reduzierten Gleichung besonders einfach. Wir betrachten dies exemplarisch an der Gleichung

$\displaystyle 2f_x + 3f_y - f_z = e^{x+y} .$

Die reduzierte Gleichung ist $ 2f_x + 3f_y - f_z= 0 .$ Das charakteristische System hat die Gestalt

$\displaystyle x'(t) = 2 , y'(t) = 3 , z'(t) = -1 .$

Das System der Phasen - DGL (unter Verwendung, daß $ x(t)$ umkehrbar ist) ist

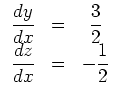
$\displaystyle \begin{array}{ccc} \displaystyle \frac{dy}{dx} & = & \displaystyl... ...\\ \displaystyle \frac{dz}{dx} & = & - \displaystyle \frac{1}{2} \end{array} $

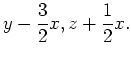
Erste Integrale sind dann $ y - \displaystyle \frac{3}{2}x, z + \displaystyle \frac{1}{2}x .$

Jede Funktion der Form 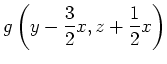$ \displaystyle g\left(y - \frac{3}{2}x, z + \frac{1}{2}x \right)$ ist eine Lösung der reduzierten Gleichung, die mit der homogenen Gleichung der Ausgangsgleichung übereinstimmt.

Eine partikuläre Lösung der Ausgangsgleichung kann man auch durch einen speziellen Ansatz (gemäß der rechten Seite) gewinnen. Setzt man $ f = a e^{x+y} ,$ dann folgt

$\displaystyle 2a e^{x+y} + 3a e^{x+y} = e^{x+y} $

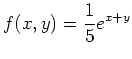und $ f(x,y) = \displaystyle \frac{1}{5} e^{x+y}$ ist eine partikuläre Lösung der PDG.

(Aus: Vorlesungsskript HM3)

siehe auch:

  automatisch erstellt am 25.  1. 2006