Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Polynom ungeraden Grades

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Warum hat ein reelles Polynom ungeraden Grades stets wenigstens eine Nullstelle?

Lösung.

Sei $ \mbox{$f:\mathbb{R}\to\mathbb{R}$}$ gegeben durch $ \mbox{$f(x) = a_m x^m + a_{m-1} x^{m-1} + \cdots + a_0 x^0$}$, wobei $ \mbox{$m$}$ ungerade sei und $ \mbox{$a_m\neq 0$}$. Sei ohne Einschränkung $ \mbox{$a_m = 1$}$ angenommen - die Division durch $ \mbox{$a_m$}$ ändert die Nullstellen nicht.

Es ist

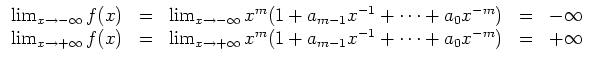
$ \mbox{$\displaystyle \begin{array}{rcrcl} \lim_{x\to -\infty} f(x) & = & \lim... ...x^m (1 + a_{m-1} x^{-1} + \cdots + a_0 x^{-m}) & = & +\infty \\ \end{array}$}$

Damit gibt es ein $ \mbox{$a\in\mathbb{R}_{< 0}$}$ mit $ \mbox{$f(a) < 0$}$ und ein $ \mbox{$b\in\mathbb{R}_{> 0}$}$ mit $ \mbox{$f(b) > 0$}$. Da $ \mbox{$f$}$ stetig ist, gibt es nach dem Zwischenwertsatz nun ein $ \mbox{$\xi\in [a,b]$}$ mit $ \mbox{$f(\xi) = 0$}$.

Die tatsächliche Berechnung einer als existent nachgewiesenen Nullstelle ist im allgemeinen nur näherungsweise möglich. Auch ist über die genaue Anzahl der Nullstellen nichts gesagt.

(Autoren: Künzer/Martin/Nebe)
[Verweise]
  automatisch erstellt am 25.  1. 2006