Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Einige Konvergenzradien

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Berechne jeweils den Konvergenzradius der Potenzreihe.

  1. $ \mbox{$\sum_{n=0}^\infty n2^n z^n$}$.
  2. $ \mbox{$\sum_{n=0}^\infty \frac{n!}{n^n}z^n$}$.
  3. $ \mbox{$\cos z=\sum_{n=0}^\infty (-1)^n \frac{z^{2n}}{(2n)!}$}$.
  4. $ \mbox{$(1+z)^\alpha=\sum_{n=0}^\infty {\alpha\choose n} z^n$}$, wobei $ \mbox{$\alpha\in\mathbb{C}$}$.
  5. $ \mbox{$\sum_{n=0}^\infty n! z^n$}$.

Lösung.

  1. Wir erhalten
    $ \mbox{$\displaystyle R\; = \; 1/(\overline {\lim}_{n\to\infty}\sqrt[n]{\vert ... ...ert}) \; = \; 1/(\overline {\lim}_{n\to\infty}2\sqrt[n]{n}) \; = \; 1/2 \; . $}$

  2. Es wird
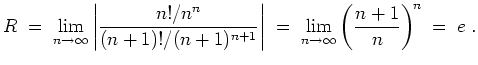
    $ \mbox{$\displaystyle R\; = \; \lim_{n\to\infty}\left\vert\frac{n!/n^n}{(n+1)!... ...vert\; =\; \lim_{n\to\infty}\left(\frac{n+1}{n}\right)^{\! n} \; = \; e\; . $}$
    Alternativ ergibt sich mit der Stirlingschen Formel
    $ \mbox{$\displaystyle R\; = \; 1/(\overline {\lim}_{n\to\infty}\sqrt[n]{\vert ... ...ert}) \; = \; 1/(\overline {\lim}_{n\to\infty}\sqrt[n]{n!}/n) \; = \; e \; . $}$
  3. Es ist $ \mbox{$\cos z=\sum_{n=0}^\infty a_n z^n$}$ mit $ \mbox{$a_{2n}:=\frac{(-1)^n}{(2n)!}$}$ und $ \mbox{$a_{2n+1}:=0$}$ für $ \mbox{$n\in\mathbb{N}$}$. Mit Stirling gilt $ \mbox{$\lim_{n\to\infty}\sqrt[n]{n!}=\lim_{n\to\infty}(\sqrt[n]{n!}/n)n=\infty$}$, und es ergibt sich
    $ \mbox{$\displaystyle \begin{array}{rcl} R &=& 1/(\overline {\lim}_{n\to\infty... ...ty}\sqrt[2n]{1/(2n)!}\vspace*{1mm}\\ &=& 1/0\\ &=& \infty\; . \end{array}$}$

    Alternativ ist mit dem Quotientenkriterium, angewandt auf die Reihe $ \mbox{$\sum_{n=0}^\infty (-1)^n \frac{z^{2n}}{(2n)!}$}$,

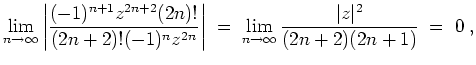
    $ \mbox{$\displaystyle \lim_{n\to\infty}\left\vert{\displaystyle\frac{(-1)^{n+1... ...m_{n\to\infty}{\displaystyle\frac{\vert z\vert^2}{(2n+2)(2n+1)}} \;=\; 0 \;, $}$
    d.h. die Reihe konvergiert für alle $ \mbox{$z\in\mathbb{C}$}$, und folglich $ \mbox{$R=\infty$}$.

  4. Im Falle $ \mbox{$\alpha\in\mathbb{N}$}$ wird $ \mbox{${\alpha\choose n}=0$}$ für $ \mbox{$n\geq\alpha+1$}$, und die (abbrechende) Reihe konvergiert für alle $ \mbox{$z\in\mathbb{C}$}$. Der Konvergenzradius ist daher gleich $ \mbox{$\infty$}$.

    Im Falle $ \mbox{$\alpha\in\mathbb{C}\backslash \mathbb{N}$}$ wird

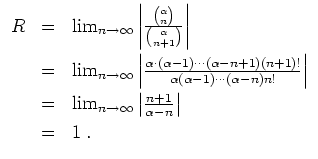
    $ \mbox{$\displaystyle \begin{array}{rcl} R &=& \lim_{n\to\infty}\left\vert\fra... ...ft\vert\frac{n+1}{\alpha-n}\right\vert\vspace*{1mm}\\ &=& 1\; . \end{array}$}$

  5. Es wird
    $ \mbox{$\displaystyle R\; = \; 1/(\overline {\lim}_{n\to\infty}\sqrt[n]{\vert n!\vert}) \; = \; 1/\infty \; = \; 0 \; . $}$

    Alternativ wird

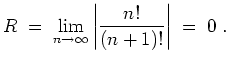
    $ \mbox{$\displaystyle R \;=\; \lim_{n\to\infty}\left\vert{\displaystyle\frac{n!}{(n+1)!}}\right\vert \;=\; 0 \;. $}$

(Autoren: Künzer/Martin/Nebe)
[Verweise]
  automatisch erstellt am 25.  1. 2006