
Mathematik-Online-Lexikon:

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: | |
Logarithmusreihe |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
Entwickle
![]() unter Zuhilfenahme der geometrischen Reihe um den Entwicklungspunkt
unter Zuhilfenahme der geometrischen Reihe um den Entwicklungspunkt
![]() in eine Potenzreihe.
Für welche
in eine Potenzreihe.
Für welche
![]() konvergiert diese Potenzreihe?
konvergiert diese Potenzreihe?
Lösung.
Es wird mit der geometrischen Reihe für
![]()
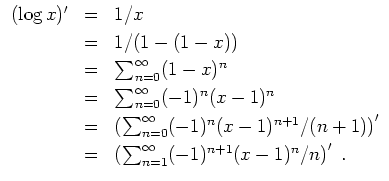
Somit ist
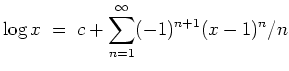
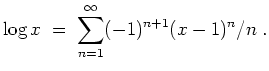
Die so erhaltene Potenzreihe hat den Konvergenzradius
![$ \mbox{$\displaystyle
R\;=\; \frac{1}{\overline {\lim}_{n\to\infty}\sqrt[n]{\vert(-1)^{n+1}/n\vert}} \;=\; 1 \;.
$}$](/inhalt/beispiel/beispiel949/img11.png)
Folglich konvergiert die Potenzreihe für
![]() und divergiert für
und divergiert für
![]() .
Für
.
Für
![]() divergiert sie als harmonische Reihe. Für
divergiert sie als harmonische Reihe. Für
![]() konvergiert sie mit dem Leibnizkriterium.
konvergiert sie mit dem Leibnizkriterium.
Insbesondere haben wir
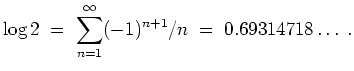
siehe auch:
| automatisch erstellt am 25. 1. 2006 |