Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Konvergenz und absolute Konvergenz

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Untersuche das uneigentliche Integral 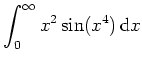$ \mbox{$\displaystyle\int _0^\infty x^2\sin(x^4)\,{\mbox{d}}x$}$ auf Konvergenz und auf absolute Konvergenz.

Lösung.

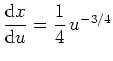
Wir wollen zeigen, daß das Integral konvergiert. Es wird zunächst mit der Substitution $ \mbox{$u = x^4$}$ und $ \mbox{${\displaystyle\frac{{\mbox{d}}x}{{\mbox{d}}u}} = {\displaystyle\frac{1}{4}}\, u^{-3/4}$}$

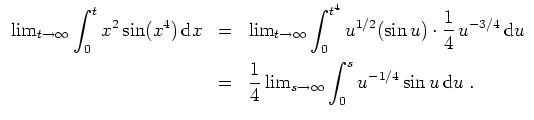
$ \mbox{$\displaystyle \begin{array}{rcl} \lim_{t\to\infty}\displaystyle\int _0... ...infty}\displaystyle\int _0^s u^{-1/4}\sin u\,{\mbox{d}}u\; . \\ \end{array}$}$
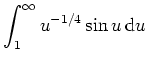Die Funktion $ \mbox{$u^{-1/4}\sin u$}$ ist in $ \mbox{$u = 0$}$ stetig durch $ \mbox{$0$}$ fortsetzbar. Um die Konvergenz zu erhalten, genügt es also, das Integral $ \mbox{$\displaystyle\int _1^\infty u^{-1/4}\sin u\,{\mbox{d}}u$}$ als konvergent nachzuweisen. In der Tat wird
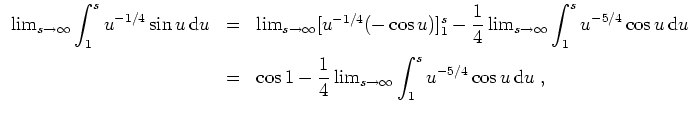
$ \mbox{$\displaystyle \begin{array}{rcl} \lim_{s\to\infty}\displaystyle\int _1... ...infty}\displaystyle\int _1^s u^{-5/4}\cos u\,{\mbox{d}}u\; , \\ \end{array}$}$
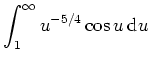und $ \mbox{$\displaystyle\int _1^\infty u^{-5/4}\cos u\,{\mbox{d}}u$}$ konvergiert sogar absolut wegen der konvergenten Majorante $ \mbox{$\vert u^{-5/4}\cos u\vert \leq u^{-5/4}$}$ für $ \mbox{$u\in\mathbb{R}_{> 1}$}$.

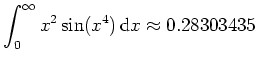Es wird übrigens $ \mbox{$\displaystyle\int _0^\infty x^2\sin(x^4)\,{\mbox{d}}x \approx 0.28303435$}$.

Wir wollen nun zeigen, daß das Integral nicht absolut konvergiert. Hierzu schätzen wir das Integral des Betrages nach unten ab. Für $ \mbox{$N\in\mathbb{Z}_{\geq 0}$}$ wird

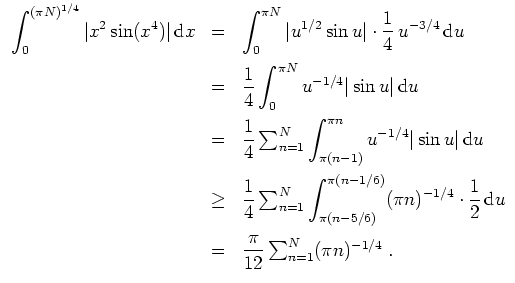
$ \mbox{$\displaystyle \begin{array}{rcl} \displaystyle\int _0^{(\pi N)^{1/4}} ... ...displaystyle\frac{\pi}{12}}\sum_{n = 1}^N (\pi n)^{-1/4}\; . \\ \end{array}$}$
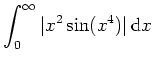Wäre $ \mbox{$\displaystyle\int _0^\infty \vert x^2\sin(x^4)\vert\,{\mbox{d}}x$}$ konvergent, so würde also $ \mbox{$\sum_{n = 1}^N (\pi n)^{-1/4}$}$ für $ \mbox{$N\to\infty$}$ gegen einen endlichen Wert konvergieren. Dies ist nicht der Fall, und damit ist das zu betrachtende Integral nicht absolut konvergent.

Skizze.

\includegraphics[width = 16cm, height = 12cm]{l3.eps}
(Autoren: Künzer/Martin/Nebe)
[Verweise]
  automatisch erstellt am 25.  1. 2006