Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon:

Ein uneigentliches Integral

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

(1)
Untersuche das Integral $ \mbox{$\displaystyle\int _0^\infty{\displaystyle\frac{\arctan x}{x^{3/2}}}\,{\mbox{d}}x$}$ mit dem Majorantenkriterium auf Konvergenz.
(2)
Berechne mittels partieller Integration und nachfolgender Substitution $ \mbox{$u = x^{1/2}$}$ seinen Wert.

Lösung.

(1)
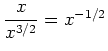Auf $ \mbox{$(0,1]$}$ ist $ \mbox{${\displaystyle\frac{x}{x^{3/2}}} = x^{-1/2}$}$ eine Majorante des Integranden $ \mbox{${\displaystyle\frac{\arctan x}{x^{3/2}}}$}$, da $ \mbox{$0 = \arctan 0$}$ und da auf $ \mbox{$[0,1]$}$ $ \mbox{$x' = 1 \geq (1 + x^2)^{-1} = (\arctan x)'$}$ gilt; und es ist $ \mbox{$\int_0^1 x^{-1/2}{\mbox{d}}x = 2$}$ konvergent. Also konvergiert auch $ \mbox{$\int_0^1 (\arctan x) \cdot x^{-3/2}\,{\mbox{d}}x$}$.

Auf $ \mbox{$[1,\infty)$}$ ist $ \mbox{${\displaystyle\frac{\pi/2}{x^{3/2}}}$}$ eine Majorante des Integranden $ \mbox{${\displaystyle\frac{\arctan x}{x^{3/2}}}$}$, da $ \mbox{$0\leq\arctan x\leq\pi/2$}$; und es ist $ \mbox{$\int_1^\infty x^{-3/2}{\mbox{d}}x = 2$}$ konvergent. Also konvergiert auch $ \mbox{$\int_1^\infty (\arctan x) \cdot x^{-3/2}\,{\mbox{d}}x$}$.

Insgesamt ist somit $ \mbox{$\int_0^\infty (\arctan x) \cdot x^{-3/2}\,{\mbox{d}}x$}$ als konvergent nachgewiesen.

(2)
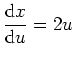Partielle Integration und Substitution $ \mbox{$u = x^{1/2}$}$, mit $ \mbox{${\displaystyle\frac{{\mbox{d}}x}{{\mbox{d}}u}} = 2u$}$, geben
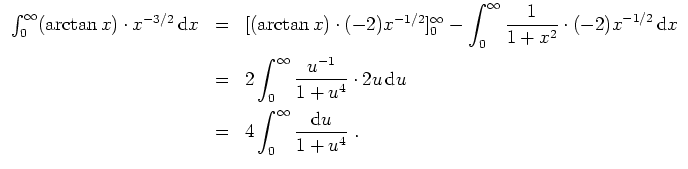
$ \mbox{$\displaystyle \begin{array}{rcl} \int_0^\infty (\arctan x) \cdot x^{-3... ...\int _0^\infty {\displaystyle\frac{{\mbox{d}}u}{1+u^4}} \; . \\ \end{array}$}$
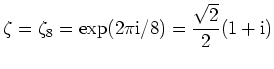Sei $ \mbox{$\zeta = \zeta_8 = \exp(2\pi\mathrm{i}/8) = {\displaystyle\frac{\sqrt{2}}{2}}(1+\mathrm{i})$}$. Es ist
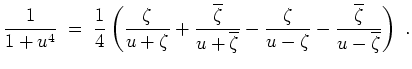
$ \mbox{$\displaystyle {\displaystyle\frac{1}{1+u^4}} \; =\; {\displaystyle\fr... ... - {\displaystyle\frac{\overline {\zeta}}{u-\overline {\zeta}}} \right)\; . $}$
Wir erhalten also
$ \mbox{$\displaystyle \begin{array}{rcl} \int_0^\infty (\arctan x) \cdot x^{-3... ...} - 1)\right]_0^\infty \vspace*{2mm}\\ & = & \pi\sqrt{2}\;.\\ \end{array}$}$
(Autoren: Künzer/Martin/Nebe)
[Verweise]
  automatisch erstellt am 25.  1. 2006