
Mathematik-Online-Lexikon: Erläuterung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Lexikon: Erläuterung zu | |
Resultante |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z | Übersicht |
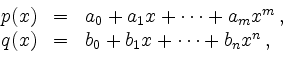
ist die Determinante der Matrix
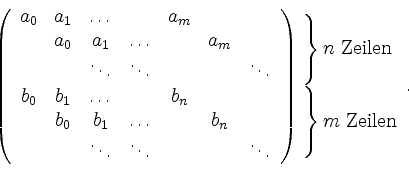
Sie ist genau dann Null, wenn die beiden Polynome eine gemeinsame Nullstelle haben.
(A)
![]() ,
,
(B)
![]() ,
,
zu der folgenden dritten Aussage gezeigt:
(C) ![]() nichttriviale
Polynome
nichttriviale
Polynome ![]() ,
, ![]() vom Grad
vom Grad ![]() bzw.
bzw. ![]() mit
mit
![]() .
.
Dazu werden die einzelnen Implikationen separat betrachtet.
(A) ![]() (C):
Aus
(C):
Aus
![]() folgt
folgt
(C) ![]() (A):
Nimmt man an, dass
(A):
Nimmt man an, dass
(B)
![]() (C):
Die Determinante
(C):
Die Determinante
![]() ist genau
dann Null, wenn das homogene lineare
Gleichungssystem
ist genau
dann Null, wenn das homogene lineare
Gleichungssystem
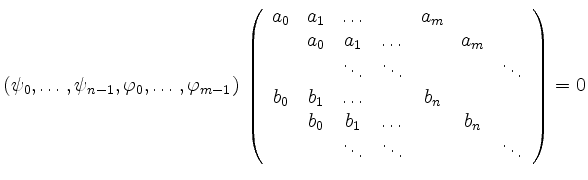
| 0 | |||
| 0 | |||
| 0 |
| automatisch erstellt am 27. 11. 2007 |