Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Eigenschaften der Ordnungsrelation

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

$ \forall$ a,b,c $ \in \mathbb{R}$ gilt:

(i)
$ a < b \quad \land \quad b < c \quad \Longrightarrow \quad a < c$ (Transitivität)

(ii)
$ a < b \quad \Longrightarrow \quad a+c < b+c$

(iii)
$ a < b \quad \land \quad c > 0 \quad \Longrightarrow \quad ac < bc$

(iv)
$ \forall$ a $ \in {\mathbb{R}}$ $ \exists$ n $ \in {\mathbb{N}} \ \ n > a$ (Achimedisches Prinzip)

(v)
$ a < b \quad \land \quad c < d \quad \Longrightarrow \quad a+c < b+d$

(vi)
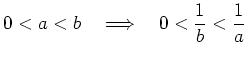
$ \displaystyle 0 < a < b \quad \Longrightarrow \quad 0 < \frac{1}{b} < \frac{1}{a}$

(vii)
Ist $ a > 0$ und $ b > 0$, dann gilt $ a < b \quad \Longleftrightarrow \quad a^2 < b^2$.

z.z.: Ist $ a > 0$ und $ b > 0$, dann gilt $ a < b \quad \Longleftrightarrow \quad a^2 < b^2$.

Beweis:

Gilt $ a < b$, so erhält man hieraus wegen $ a > 0$ nach (iii) durch Multiplikation mit $ a$ die Ungleichung $ a^2 < ab$. Analog bekommt man nach Multiplikation mit $ b$ den Ausdruck $ ab < b^2$. Mit der Transitivität folgt dann $ a^2 < b^2$.

Nun sei vorausgesetzt, daß $ a^2 < b^2$ und $ a,b > 0 .$ Wenn $ a > b$ wäre, so würde man wie oben zu der Ungleichung $ a^2 > b^2$ gelangen, im Widerspruch zur Voraussetzung. Ist $ a = b $, dann gilt $ a^2 = b^2 .$ Es muß also $ a < b$ sein.

(Aus: Lineare Algebra und Geometrie, Kimmerle)
[Zurück zur Aussage]
  automatisch erstellt am 25.  1. 2006