Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon: Erläuterung zu

Lineares Programm

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Die Minimierung einer linearen Funktion

$\displaystyle (c_1, \dots, c_n)x \mapsto \textrm{min} $

unter linearen Nebenbedingungen

$\displaystyle Ax \ge b $

mit einer $ m\times n$-Matrix $ A$ bezeichnet man als lineares Programm. Eine Lösung $ x_\star \in \mathbb{R}^n$ erfüllt die Kuhn-Tucker-Bedingung, falls

$\displaystyle c^{\text{t}}=\lambda^{\text{t}}A, \quad \lambda^{\text{t}}(Ax_\star-b)=0 $

mit $ \lambda_i \ge 0$. Für ein Maximun gilt entsprechend $ \lambda_i \le 0$.

Für das konkrete Beispiel

$\displaystyle x+y \mapsto$   min$\displaystyle , \quad x+2y \ge 8, x\ge4, y\ge 3 $

ist

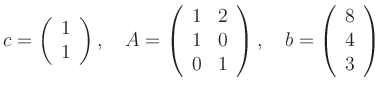
$\displaystyle c= \left( \begin{array}{c} 1 \\ 1 \\ \end{array} \right),... ...uad b= \left( \begin{array}{c} 8 \\ 4 \\ 3 \\ \end{array} \right) $

und man erhält die Kuhn-Tucker-Bedingung

$\displaystyle 1=\lambda+\varsigma, 1=2\varsigma+\delta $

$\displaystyle \lambda[x+2y-8] \mp \varsigma[x-4]=\delta[y-3]=0 $

mit $ \lambda$, $ \varsigma$, $ \delta$, $ [\dots]$ $ \geq 0$. Man erkennt schnell, dass genau einer der Lagrange-Multiplikator gleich Null sein muss. Für die drei Fälle sind dann jeweils zwei Nebenbedingungen aktiv. Diese legen $ x$ und $ y$ eindeutig fest:

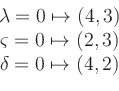
\begin{displaymath} \begin{array}{c} \lambda = 0 \mapsto (4,3) \\ \varsigm... ...\mapsto (2,3) \\ \delta = 0 \mapsto (4,2) \\ \end{array} \end{displaymath}

Vergleich der Zielfunktionswerte $ x+y$ zeigt, dass das Minimum bei $ (2,3)$ angenommen wird. Die zugehörigen Lagrange-Multiplikatoren sind $ \lambda=1$, $ \delta=1$.

\includegraphics[width=0.4\linewidth]{Bild_Lineares_Programm}

Eine geometrische Konstruktion der Lösung ist in der Abbildung illustriert. Die Lösung $ (2,3)$ ist der Punkt in dem eine Niveaugerade der Zielfunktion den schraffierten zulässigen Bereich berührt. Es ist offensichtlich, dass die Zielfunktion ansteigt (fällt), wenn die Niveaugeraden den zulässigen Bereich schneiden (nicht schneiden).

Sind die Zeilen von $ A$, die mit positiven $ \lambda_i$ multipliziert werden, linear unabhängig, folgt die Charakterisierung unmittelbar aus den Kuhn-Tucker-Bedingungen im allgemeinen nichtlinearen Fall. Da im linearen Fall linear abhängige Gleichungen redundant sind, können sie weggelassen werden, und man kann sich auf den nicht-degenerierten Fall beschränken.
[Zurück]
  automatisch erstellt am 26.  1. 2017