Ist 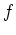 bis auf
endlich viele schwache
Singularitäten analytisch in einem Gebiet
bis auf
endlich viele schwache
Singularitäten analytisch in einem Gebiet 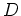 ,
dann gilt
für jede geschlossene Kurve
,
dann gilt
für jede geschlossene Kurve 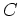 , die in
, die in 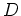 zu einem
Punkt homotop ist.
zu einem
Punkt homotop ist.
Zur Illustration der Beweisidee wird angenommen,
dass die Kurve 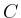 ein Rechteck
ein Rechteck 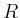 in
in 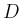 berandet und
berandet und 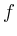 analytisch ist.
analytisch ist.
Im Folgenden wird die Abkürzung
für das Integral über den entgegen dem Uhrzeigersinn orientierten
Rand eines Rechtecks verwendet.
Das Rechteck 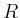 wird nun in vier kongruente Rechtecke
wird nun in vier kongruente Rechtecke 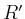 ,
, 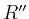 ,
,
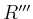 und
und 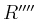 aufgeteilt, und es folgt
aufgeteilt, und es folgt
da sich die Integrale auf den mehrfach durchlaufenen Wegstücken aufheben.
Es ist klar, dass für mindestens eines dieser Teil-Rechtecke (im Folgenden mit
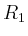 bezeichnet)
bezeichnet)
gilt. Iteriert man diesen Prozess, so erhält man eine Folge
mit
Die Folge dieser Rechtecke 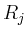 konvergiert gegen einen Punkt
konvergiert gegen einen Punkt 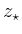 ,
d.h.
,
d.h.

für
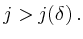
Da 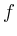 komplex differenzierbar ist, gilt weiter
komplex differenzierbar ist, gilt weiter
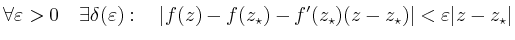
für
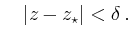
Mit Hilfe von
erhält man für
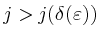
wobei 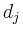 die Länge der Diagonale und
die Länge der Diagonale und 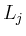 die Länge des Randes von
die Länge des Randes von 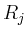 bezeichnet. Für das ursprüngliche Integral folgt damit
bezeichnet. Für das ursprüngliche Integral folgt damit
und da
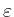 beliebig gewählt war,
beliebig gewählt war,
Der allgemeine Fall erfordert noch einige
zusätzliche Überlegungen,
bei denen insbesondere die topologische Form des Gebietes 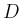 berücksichtigt
werden muss.
berücksichtigt
werden muss.
| |
automatisch erstellt
am 21. 11. 2013 |


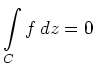
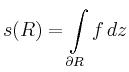
![\includegraphics[width=.3\linewidth]{e_cauchy}](/inhalt/erlaeuterung/erlaeuterung444/img6.png)
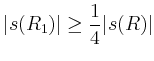
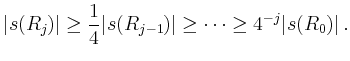
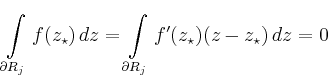
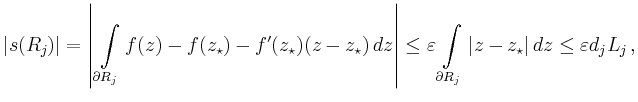
![]() berücksichtigt
werden muss.
berücksichtigt
werden muss.