Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Residuum

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Für eine in einer punktierten Kreisscheibe $ D\backslash\{a\}$ analytische Funktion $ f$ definiert man das Residuum im Punkt $ a$ als

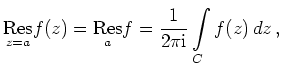
$\displaystyle \underset{z=a}{\operatorname{Res}}f(z) =\underset{a}{\operatorname{Res}}f= \frac{1}{2\pi\mathrm{i}} \int\limits_C f(z)\,dz \,, $

wobei $ C\subset D\backslash\{a\}$ ein geschlossener Weg mit $ n(C,a)=1$ ist (z. B. ein entgegen dem Uhrzeigersinn durchlaufener Kreis).

\includegraphics[width=.5\moimagesize]{a_residuum}

Ist $ a$ eine Polstelle $ n$-ter Ordnung, d.h. gilt

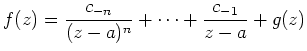
$\displaystyle f(z) = \frac{c_{-n}}{(z-a)^n} + \cdots + \frac{c_{-1}}{z-a} + g(z) $

mit $ \vert g(z)\vert=O(1)$ für $ z\to a$, so ist

$\displaystyle \underset{a}{\operatorname{Res}}f = c_{-1} \,. $

Dies gilt allgemeiner für eine absolut konvergente Laurent-Reihe

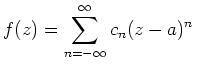
$\displaystyle f(z) = \sum_{n=-\infty}^\infty c_n (z-a)^n\, $

in der Umgebung einer wesentlichen Singularität.

Aus Cauchys Theorem folgt, dass die Definition von $ \underset{a}{\operatorname{Res}}f$ unabhängig von der gewählten Kurve $ C$ ist.

Die äquivalenten Definitionen für eine Polstelle und eine Laurent-Reihe folgen, da die Funktionen $ g(z)$ und $ (z-a)^n$, $ n\neq -1$, in einer Kreisscheibe um $ a$ Stammfunktionen besitzen, und damit ihr Integral über den geschlossenen Weg $ C$ null ist. Nach Definition der Umlaufzahl gilt

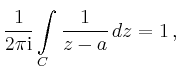
$\displaystyle \frac{1}{2\pi\mathrm{i}}\int\limits_C \frac{1}{z-a}\,dz = 1\,, $

was sich für einen Kreis auch unmittelbar nachrechnen lässt.

[Zurück]
  automatisch erstellt am 21. 11. 2013