Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Residuensatz

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Sei $ C$ der entgegen dem Uhrzeigersinn orientierte Rand eines beschränkten Gebietes $ D$.

\includegraphics[width=0.5\linewidth]{a_residuensatz}

Dann gilt für eine in $ \overline{D}$ stetige und in $ D$ bis auf endlich viele Singularitäten $ a_j$ analytische Funktion $ f$

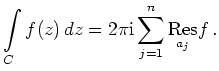
$\displaystyle \int\limits_C f(z)\,dz = 2\pi\mathrm{i} \sum_{j=1}^n \underset{a_j}{\operatorname{Res}}f \,. $

\includegraphics[width=0.5\linewidth]{e_residuensatz}

Betrachtet man für jede Singularität $ a_j$ ( $ j=1,\cdots,n$) einen im Uhrzeigersinn orientierten Kreis $ C_j$ um $ a_j$, der ganz in $ D$ liegt und in dessen Innerem sich keine andere Singularität befindet, so gilt nach Cauchys Theorem

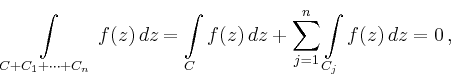
$\displaystyle \int\limits_{C+C_1+\cdots+C_n} f(z)\,dz =\int\limits_C f(z)\,dz +\sum_{j=1}^n \int\limits_{C_j}f(z)\,dz =0\,, $

denn $ f$ ist analytisch im Inneren des von $ C+C_1+\cdots+C_n$ berandeten Teilgebiets.

Andererseits gilt für jeden Weg $ C_j$

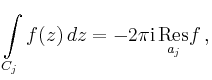
$\displaystyle \int\limits_{C_j}f(z)\,dz= -2\pi\mathrm{i}\,\underset{a_j}{\operatorname{Res}}f\,, $

da die Wege $ C_j$ im Uhrzeigersinn orientiert sind. Durch Einsetzen in die obige Gleichung erhält man schließlich

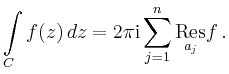
$\displaystyle \int\limits_C f(z)\,dz = 2\pi\mathrm{i} \sum_{j=1}^n \underset{a_j}{\operatorname{Res}}f \,. $

[Zurück]
  automatisch erstellt am 21. 11. 2013