Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Komplexe Taylor-Reihe

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Eine in einem Gebiet $ D$ analytische Funktion $ f$ lässt sich in jedem Punkt $ a\in D$ in eine Taylor-Reihe entwickeln:

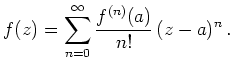
$\displaystyle f(z) = \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!} \,(z-a)^n \,. $

Die Reihe konvergiert absolut für

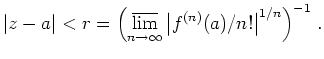
$\displaystyle \vert z-a\vert < r = \left( \operatorname*{\overline{lim}}_{n\rightarrow\infty} \left\vert f^{(n)}(a) / n! \right\vert^{1/n} \right)^{-1} \,. $

Dieser Konvergenzradius $ r$ ist gleich dem Abstand des Entwicklungspunktes $ a$ zur nächsten Singularität von $ f$, d.h. zum Rand des Analytizitätsgebietes.
Sei $ C$ ein entgegen dem Uhrzeigersinn durchlaufener Kreis um $ a$ mit Radius $ s$ und

$\displaystyle \vert z-a\vert < s < r \,, $

dann folgt aus der Integraldarstellung

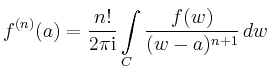
$\displaystyle f^{(n)}(a) =\frac{n!}{2\pi\mathrm{i}}\int\limits_C \frac{f(w)}{(w-a)^{n+1}}\,dw $

die Abschätzung

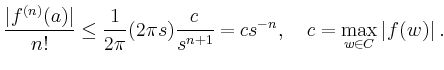
$\displaystyle \frac{\vert f^{(n)}(a)\vert}{n!} \le \frac{1}{2\pi} (2\pi s) \frac{c}{s^{n+1}}= c s^{-n},\quad c = \max_{w\in C} \vert f(w)\vert \,. $

Damit ist der Betrag der Summanden in der Taylor-Reihe $ \le c (\vert z-a\vert/s)^n \,,$ die Reihe wird also durch eine konvergente geometrische Reihe majorisiert. Da $ s<r$ beliebig wählbar ist, erhält man Konvergenz auf der größten in $ D$ enthaltenen offenen Kreisscheibe.

Wie man leicht sieht, ist das Konvergenzgebiet maximal. Für $ \vert z-a\vert$ größer als der Abstand $ r$ von $ a$ zum Rand des Analytizitätsgebietes divergiert die Taylor-Reihe. Aus absoluter Konvergenz würde nämlich folgen, dass die offene Kreisscheibe mit Radius $ \vert z-a\vert$ zum Konvergenzgebiet gehört. Dies beweist ebenfalls die Äquivalenz zu der aus der Theorie reeller Reihen bekannten expliziten Formel für $ r$.

[Zurück]
  automatisch erstellt am 21. 11. 2013