Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Laurent-Reihe

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Eine in einem Kreisring

$\displaystyle D:\ r_1 < \vert z-a\vert < r_2 $

analytische Funktion $ f$ kann in eine Laurent-Reihe

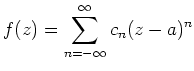
$\displaystyle f(z) = \sum_{n=-\infty}^\infty c_n (z-a)^n $

entwickelt werden, die in $ D$ absolut konvergiert. Die Koeffizienten besitzen die Integraldarstellung

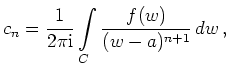
$\displaystyle c_n = \frac{1}{2\pi\mathrm{i}} \int\limits_C \frac{f(w)}{(w-a)^{n+1}}\,dw \,, $

wobei $ C\subset D$ ein beliebiger entgegen dem Uhrzeigersinn durchlaufener Kreis um $ a$ ist.

Die Laurent-Reihe entspricht einer Zerlegung

$\displaystyle f(z) = f_1(z-a) + f_2(1/(z-a)) $

von $ f$ in zwei analytische Funktionen $ f_j$, die bis auf eine Konstante eindeutig bestimmt sind. Die Konvergenzgebiete von $ f_1$ und $ f_2$ sind offene Kreisscheiben um $ a$ mit Radius $ r_2$ bzw. $ 1/r_1$.
Zur Vereinfachung wird der Entwicklungspunkt $ a$ in den Ursprung verschoben ($ a=0$). Nun wählt man, wie in der Abbildung skizziert, zwei Kreise, die den Punkt $ z$ einschließen.

\includegraphics[width=.4\linewidth]{e_laurentreihe}

Dann gilt nach der Cauchyschen Integralformel

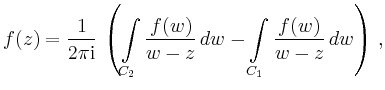
$\displaystyle f(z) = \frac{1}{2\pi\mathrm{i}}\, \left( \int\limits_{C_2} \frac{f(w)}{w-z}\,dw - \int\limits_{C_1} \frac{f(w)}{w-z}\,dw \right) \,, $

wobei das Minuszeichen die Orientierung von $ C_1$ umkehrt; $ C_2-C_1$ ist der orientierte Rand eines Kreisrings, der $ z$ enthält.

In dem ersten Integral ersetzt man $ 1/(w-z)$ durch

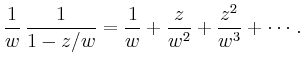
$\displaystyle \frac{1}{w}\,\frac{1}{1-z/w} = \frac{1}{w} + \frac{z}{w^2} + \frac{z^2}{w^3} + \cdots \,. $

Da $ \vert z\vert<\vert w\vert$ für $ w\in C_2$, ist diese geometrische Reihe absolut konvergent. Im zweiten Integral ist $ \vert z\vert>\vert w\vert$, und man verwendet die Entwicklung

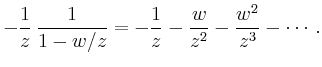
$\displaystyle -\frac{1}{z}\,\frac{1}{1-w/z} = -\frac{1}{z}-\frac{w}{z^2}-\frac{w^2}{z^3}-\cdots\,. $

Man kann also die beiden Integrale durch die Summen

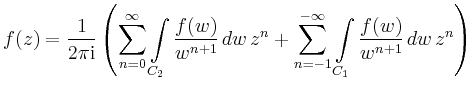
$\displaystyle f(z)=\frac{1}{2\pi\mathrm{i}}\left(\sum_{n=0}^\infty \int\limits_... ...\sum_{n=-1}^{-\infty} \int\limits_{C_1} \frac{f(w)}{w^{n+1}}\,dw\, z^n \right) $

darstellen.

Berücksichtigt man, dass sich der Integrationsweg für die auf $ D$ analytische Funktion $ f(w)/w^{n+1}$ verschieben lässt, so ergibt sich die angegebene Formel für die Koeffizienten.

Das obige Argument zeigt ebenfalls die Aufspaltung in die zwei analytischen Funktionen $ f_j$. Deren Eindeutigkeit folgt aus der Eindeutigkeit der Laurent-Entwicklung. Ihre Koeffizienten sind durch die Integralformel gegeben.

[Zurück]
  automatisch erstellt am 21. 11. 2013