Eine lineare partielle Differentialgleichung zweiter Ordnung
für eine zweimal stetig differenzierbare Funktion
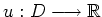 mit
mit
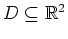 hat die Gestalt
hat die Gestalt
Man beachte, daß
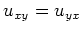 , da
, da 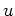 von Klasse
von Klasse 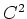 ist.
Die Diskriminante
einer solchen PDG ist definiert als
ist.
Die Diskriminante
einer solchen PDG ist definiert als
Die partielle Differentialgleichung heißt

- a)
- Die Wellengleichung
besitzt die Diskriminante
ist also hyperbolisch.
- b)
- Die Gleichung
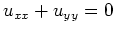 ist elliptisch (
ist elliptisch (
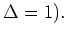 Man nennt sie die Potentialgleichung. Ein ebenes elektrostatisches Potential erfüllt diese Gleichung.
Man nennt sie die Potentialgleichung. Ein ebenes elektrostatisches Potential erfüllt diese Gleichung.
- c)
- Die Funktion
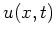 beschreibe im Punkt
beschreibe im Punkt 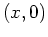 der
der 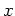 - Achse
die Temperatur zur Zeit
- Achse
die Temperatur zur Zeit 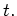 Sie erfüllt die PDG
Man nennt sie Diffusionsgleichung.
Diese Gleichung ist Beispiel einer parabolischen PDG (
Sie erfüllt die PDG
Man nennt sie Diffusionsgleichung.
Diese Gleichung ist Beispiel einer parabolischen PDG (
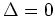 ).
In der Form
nennt man sie
Wärmeleitungsgleichung.
Die
).
In der Form
nennt man sie
Wärmeleitungsgleichung.
Die 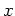 - Achse wird hierbei als Stab interpretiert und
- Achse wird hierbei als Stab interpretiert und 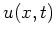 gibt die Temperaturverteilung im Stab an.
Die Störfunktion
gibt die Temperaturverteilung im Stab an.
Die Störfunktion 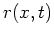 beschreibt den Temperatureinfluß von außen.
beschreibt den Temperatureinfluß von außen.
- d)
- Bei konstanten Koeffizienten ist die Diskriminante unabhängig
von
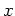 und
und 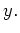 Im Allgemeinen wird dies nicht der Fall sein. Man präzisiert
dann die Definition dadurch, daß man sagt, daß die gegebene PDG in
Im Allgemeinen wird dies nicht der Fall sein. Man präzisiert
dann die Definition dadurch, daß man sagt, daß die gegebene PDG in
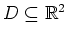 (
( wird in der Regel verlangt) hyperbolisch bzw.
parabolisch bzw. elliptisch ist, wenn in allen Punkten
wird in der Regel verlangt) hyperbolisch bzw.
parabolisch bzw. elliptisch ist, wenn in allen Punkten 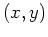 von
von 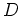 die
Diskriminante
die
Diskriminante
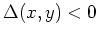 bzw.
bzw. 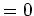 bzw.
bzw. 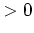 ist.
ist.
- e)
- Eine PDG 2. Ordnung, die in
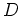 weder hyperbolisch noch parabolisch
noch elliptisch ist, nennt man von gemischtem Typ.
weder hyperbolisch noch parabolisch
noch elliptisch ist, nennt man von gemischtem Typ.
- f)
- Die Typenbezeichnungen der PDG 2. Ordnung stammen aus der Geometrie.
Ein Kegelschnitt mit der Gleichung
hat bezüglich der Koeffizienten die entsprechenden Eigenschaften, wenn er eine Hyperbel, Parabel oder
Ellipse ist (die Umkehrung ist allerdings nicht richtig).
(Aus: Vorlesungsskript HM3)
| |
automatisch erstellt
am 25. 1. 2006 |


![]() , da
, da ![]() von Klasse
von Klasse ![]() ist.
Die Diskriminante
einer solchen PDG ist definiert als
ist.
Die Diskriminante
einer solchen PDG ist definiert als
