Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Entwicklung einer Differentialgleichung im regulären Punkt

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Die Differentialgleichung

$\displaystyle r(z) u''(z) + q(z) u'(z) + p(z) u(z) = 0 $

ist bei $ z=a$ regulär, wenn $ q/r$ und $ p/r$ in einer Umgebung von $ a$ analytisch sind.

In einem regulären Punkt $ a$ exisitiert zu beliebigen Werten $ u(a)=u_0$, $ u'(a)=u_1$ eine eindeutige, in einer Umgebung von $ a$ analytische Lösung $ u$.
Insbesondere existieren zwei linear unabhängige Lösungen zu den Werten

$\displaystyle u(a)=0,\quad u'(a)=1 $

und

$\displaystyle u(a) =1 ,\quad u'(a)=0\, . $

Nach Division durch $ r$ kann man $ r=1$ annehmen und o. B. d. A. $ a=0$ setzen, d.h. man hat die Entwicklungen

$\displaystyle p(z) = p_0 + p_1 z + \cdots,\quad q(z) = q_0 + q_1 z + \cdots \,, $

mit $ \vert p_j\vert,\vert q_j\vert\le c s^j$ für ein $ s>0$. Der formale Ansatz

$\displaystyle u(z) = u_0 + u_1 z + \cdots +u_n z^n+\cdots\,,\quad u'(z) = u_1 +2u_2z +z + \cdots $

führt nach Koeffizientenvergleich der Entwicklungen

$\displaystyle p(z)u(z) =$ $\displaystyle \; p_0u_0+(p_1u_0+p_0u_1)z+\cdots+(p_nu_0+\cdots+p_0u_n)z^n+\cdots,$    
$\displaystyle q(z)u'(z) =$ $\displaystyle \;q_0u_1+(q_1u_1+2q_0u_2)z + \cdots$    
  $\displaystyle + (q_nu_1+2q_{n-1}u_2+\cdots+(n+1)q_0u_{n+1})z^n+\cdots,$    
$\displaystyle u''(z) =$ $\displaystyle \; 2 u_2+6u_3z+\cdots+(n+2)(n+1)u_{n+2}z^n+\cdots$    

auf die Rekursion


$\displaystyle 2u_2 =$ $\displaystyle -q_0u_1-p_0u_0\,,$    
$\displaystyle 6u_3 =$ $\displaystyle -(q_1u_1+2q_0u_2)-(p_1u_0+p_0u_1)\,,$    
$\displaystyle \vdots$      
$\displaystyle (n+2)(n+1)u_{n+2} =$ $\displaystyle -(q_nu_1+\cdots+(n+1)q_0u_{n+1}) - (p_nu_0+\cdots+p_0u_n)\,,$    
$\displaystyle \vdots$ $\displaystyle .$    

Man kann also alle Koeffizienten sukzessive aus $ u_0=u(0)$ und $ u_1=u'(0)$ berechnen. Dies zeigt insbesondere die Eindeutigkeit.

Es bleibt zu überprüfen, ob die Prozedur tatsächlich auf eine analytische Funktion führt. Dazu wird induktiv gezeigt, dass

$\displaystyle \vert u_j\vert \le d t^j $

mit noch zu wählenden positiven Konstanten $ d$ und $ t$ ist. Durch den Induktionsanfang ergibt sich für $ d$

$\displaystyle d\ge \vert u_0\vert$    und $\displaystyle \quad d \ge \vert u_1\vert/t\,. $

Für den Induktionsschritt erhält man aus der Rekursion

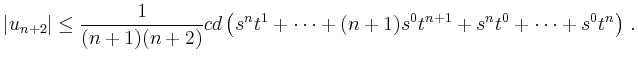
$\displaystyle \vert u_{n+2}\vert \le \frac{1}{(n+1)(n+2)}cd\left(s^nt^1+\cdots+(n+1)s^0t^{n+1} + s^nt^0+\cdots+s^0t^n\right)\,. $

Mit $ t\ge s$ und $ 1+\cdots+(n+1)=(n+1)(n+2)/2$ ergibt sich

$\displaystyle \vert u_{n+2}\vert \le cd\left(\frac{t^{n+1}}{2}+\frac{t^n}{(n+2)}\right) \le cd\left(\frac{1}{2t}+\frac{1}{t^2}\right)t^{n+2}\,. $

Dieser Ausdruck ist kleiner als $ d t^{n+2}$, wenn $ t$ so groß gewählt wird, dass

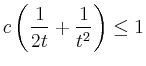
$\displaystyle c\left(\frac{1}{2t}+\frac{1}{t^2}\right)\le 1 $

gilt.

Auf diese Weise erhält man unter Umständen einen zu kleinen Konvergenzradius. Es kann gezeigt werden, dass $ t$ mit dem Minimum der Konvergenzradien von $ p$ und $ q$ übereinstimmt.

[Zurück]
  automatisch erstellt am 21. 11. 2013