Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon: Erläuterung zu

Kreis in der Gaußschen Zahlenebene

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Die Gleichung

$\displaystyle \vert z-a\vert = s \vert z-b\vert,\quad s\ne 1\, , $

beschreibt einen Kreis mit Mittelpunkt

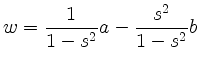
$\displaystyle w=\frac{1}{1-s^2}a-\frac{s^2}{1-s^2}b $

und Radius

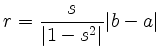
$\displaystyle r=\frac{s}{\vert 1-s^2\vert}\vert b-a\vert $

der Gaußschen Zahlenebene.

Ist $ s< 1$ so liegt $ a$ im Inneren des Kreises und $ b$ außerhalb. Für $ s > 1$ ist es umgekehrt.

\includegraphics[width=10cm]{kreis_komplexe_ebene}

Die Parameterform dieses Kreises ist

$\displaystyle w + r e^{\mathrm{i}t},\quad t\in[0,2\pi) \,. $

Deutet man die Gleichung

$\displaystyle \vert z-a\vert = s \vert z-b\vert,\quad s\ne 1\, , $

geometrisch, bedeutet sie, dass die Abstände eines Punktes $ Z$ zu zwei gegeben Punkten $ A$ und $ B$ ein festes Verhältnis $ s$ haben sollen, also

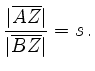
$\displaystyle \frac{\vert\overline{AZ}\vert}{\vert\overline{BZ}\vert}=s\,. $

Um festzustellen, für welche Punkte dies gilt, kann man für $ s<1$ wie folgt vorgehen.

\includegraphics[width=10cm]{kreis_des_apollonius}

Zunächst ermittelt man die Punkte $ Z_i$ und $ Z_a$ auf der Geraden $ AB$, für die gilt

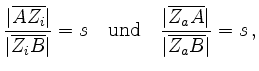
$\displaystyle \frac{\vert\overline{AZ_i}\vert}{\vert\overline{Z_iB}\vert}=s\qua... ...rm{und}\quad \frac{\vert\overline{Z_aA}\vert}{\vert\overline{Z_aB}\vert}=s\,, $

das heißt die Punkte, die die Strecke $ \overline{AB}$ innen beziehungsweise außen im Verhältnis $ s$ teilen.

Schneidet man die Gerade $ g$ durch $ Z$ und $ Z_i$ sowie die Gerade $ h$ durch $ Z$ und $ Z_a$ mit der Parallelen zur Geraden $ ZB$ durch $ A$ erhält man $ S_1$ und $ S_2$.

Mit Hilfe der Strahlensätze ergibt sich, dass

$\displaystyle \frac{\vert\overline{AS_1}\vert}{\vert\overline{BZ}\vert}= \frac{... ...ne{BZ}\vert}= \frac{\vert\overline{Z_aA}\vert}{\vert\overline{Z_aB}\vert}=s\,. $

Da vorausgesetzt ist, dass auch 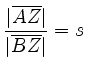$ \displaystyle \frac{\vert\overline{AZ}\vert}{\vert\overline{BZ}\vert}=s$ gilt, haben die Strecken $ \overline{AZ}, \overline{AS_1}$ und $ \overline{AS_2}$ die selbe Länge und die Geraden $ g$ und $ h$ stehen senkrecht aufeinander. Damit ist das Dreieck $ Z_aZZ_i$ rechtwinklig und alle Punkte $ Z$, für die dies gilt, liegen auf dem Kreis mit Durchmesser $ \overline{Z_aZ_i}$.

Dies hat Apollonius 200 v. Chr. bemerkt,was zur Bezeichnung Kreis des Apollonius führte.

(Autor: Jörg Hörner )
[Zurück zur Aussage]
  automatisch erstellt am 11.  6. 2007