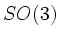 ist die Menge reeller orthogonalen 3
ist die Menge reeller orthogonalen 3 3-Matrizen mit Determinante 1.
3-Matrizen mit Determinante 1.
Typische Elemente sind die ,,Drehungen um die 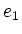 ,
, 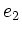 , und
, und 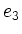 -Achse``, d.h.
-Achse``, d.h.
Zu jedem
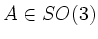 gibt es
gibt es
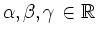 , so dass
, so dass
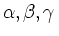 werden als ,,Eulersche Winkel`` bezeichnet.
Insbesondere wird
werden als ,,Eulersche Winkel`` bezeichnet.
Insbesondere wird 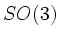 von den Drehungen
von den Drehungen 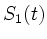 ,
, 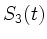 mit
mit
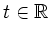 erzeugt.
erzeugt.
Es sei
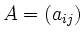 . Wir setzen
. Wir setzen
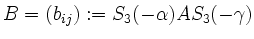 und bestimmen
und bestimmen
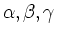 so, dass
so, dass
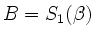 . Aus dieser Gleichung folgt:
. Aus dieser Gleichung folgt:
- Wegen
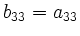 und
und
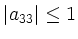 gibt es ein
gibt es ein
![$ \beta \in [0, \pi]$](/inhalt/erlaeuterung/erlaeuterung594/img7.png) ,
so dass
,
so dass
- Es gilt
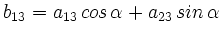 .
Es kann ein
.
Es kann ein
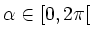 gewählt werden, so dass
gewählt werden, so dass
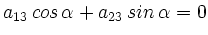 . Damit ist auch
. Damit ist auch
- Nun wählen wir ein
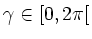 so, dass
Dies ist möglich, weil auf der rechten Seite der Gleichung insgesamt ein Vektor vom Betrag
1 steht. Daraus folgt, dass
so, dass
Dies ist möglich, weil auf der rechten Seite der Gleichung insgesamt ein Vektor vom Betrag
1 steht. Daraus folgt, dass
- Wegen der Orthogonalität von
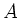 muss auch
muss auch 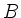 orthogonal sein, d.h. es muss gelten
orthogonal sein, d.h. es muss gelten
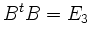 . Mit
. Mit
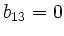 folgt daraus
Also gilt insgesamt:
folgt daraus
Also gilt insgesamt:
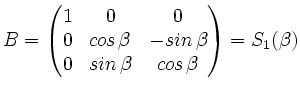 .
.
Nach Konstruktion von
 ist ausserdem die folgende Abbildung bijektiv:
ist ausserdem die folgende Abbildung bijektiv:
(Autor: Borgart)
| |
automatisch erstellt
am 13. 10. 2006 |


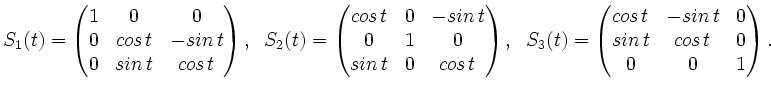
![]() gibt es
gibt es
![]() , so dass
, so dass
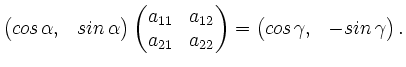
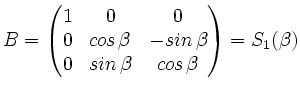 .
.