Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Eigenschaften der Max - Bedingung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Die folgenden Aussagen sind für eine Gruppe $ G$ äquivalent:
a)
$ G$ erfüllt die Max-Bedingung.
b)
Jede aufsteigende Kette von Untergruppen von $ G$ wird stationär.
c)
Jede nicht-leere Familie von Untergruppen von $ G$ besitzt ein maximales Element.
Bemerkung:

b) zeigt, wie man analog zur Max- auch eine Min-Bedingung definieren kann (jede absteigenden Kette von Untergruppen wird stationär). Gruppen die der Min-Bedingung genügen nennt man auch artinsch (nach Emil Artin (1898-1962)).

a) $ \Rightarrow$ b)
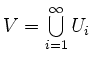Sei $ U_1 \leq U_2 \leq \ldots \leq U_i \leq \ldots$ eine aufsteigende Kette von Untergruppen. Setzt man $ V= \bigcup \limits_{i=1}^\infty U_i$, dann ist $ V$ nach dem Untergruppenkriterium eine Untergruppe von $ G$. Nach Voraussetzung ist $ V$ endlich erzeugt. Es gibt also $ g_1, \ldots g_m \in G$ mit $ V=\langle g_1 , \ldots , g_m \rangle$. Zu jedem $ g_i$ existiert ein $ U_{\alpha_i}$ mit $ g_i \in U_{\alpha_i}$ und die Menge $ \{ \alpha_1, \ldots ,\alpha_m \}$ ist endlich. Sei $ \beta=max(\alpha_1, \ldots , \alpha_m)$. Dann gilt $ g_1 , \ldots , g_m \in U_\beta$, und es ist $ \langle g_1 , \ldots ,g_m \rangle \leq U_\beta \leq V$. Also ist $ U_\beta=V$ und die aufsteigende Kette ist ab dem Index $ \beta$ konstant.

b) $ \Rightarrow$ c)
Diese Implikation folgt mit dem Lemma von Zorn.

c) $ \Rightarrow$ a)
Sei $ U \leq G$. Ist $ \vert U\vert\leq \infty$, dann ist $ U$ trivialerweise endlich erzeugt. Also kann man $ \vert U\vert=\infty$ annehmen. Sei $ \{u_i\}_{i \in \mathbb{N}}$ eine $ \infty-$liche Teilmenge von $ U$. Für $ U_i=\langle u_1, \ldots , u_i \rangle$ betrachte man die Kette

$\displaystyle U_1 \leq U_2 \leq U_3 \leq \ldots \,, $

und setze $ {\mathcal F}=\{U_i \}_{i \in {\mathbb{N}}}$. Nach $ c)$ existiert in $ {\mathcal F}$ ein maximales Element $ \widetilde{U}$, so dass $ U_i \leq \widetilde{U}$. Da $ U \in {\mathcal F}$ ist gibt es ein $ j$ mit $ \widetilde{U}=U_j$. Es gilt dann für alle $ k \geq j$ die Gleichheit $ U_k=U_j$.

Wäre nun $ U$ nicht endlich erzeugt, dann gibt es eine Menge $ \{u_i \}$, so dass Kette der zugehörigen $ U_i$ nicht stationär wird. Dies ist aber nicht möglich, und $ U$ daher endlich erzeugt.

[Zurück zur Aussage]
  automatisch erstellt am 3. 11. 2006