Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Elementarteilersatz

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Sei $ F$ eine freie abelsche Gruppe vom Rang $ n$ und $ U \leq F$. Dann gibt es eine Basis $ \{ b_1, \ldots b_n \}$ von $ F$ und $ z_1, \ldots , z_n \in \mathbb{Z} $, so dass
(i)
$ \{z_1b_1, \ldots , z_nb_n \}$ ein Erzeugendensystem von $ U$ ist.
(ii)
Die $ z_i$ kann man so nummerieren, dass $ z_i$ ein Teiler von $ z_{i+1}$ ist. Ist dann $ z_{m+1} = \ldots = z_n = 0$ und $ z_m \neq 0 ,$ dann ist $ \{ z_1b_1, \ldots, z_mb_m \}$ eine Basis von $ U .$
Die $ z_1, \ldots , z_n$ nennt man die Elementarteiler von $ U$ in $ F$. Sie sind bis auf das Vorzeichen eindeutig bestimmt.
Beweisskizze: Der Beweis des Elementarteilersatzes ist konstruktiv.

Nach den Rangbetrachtungen besitzt $ U$ eine Basis $ \{u_1, \ldots , u_m\}$, mit $ m \leq Rang(F)=n$. Es gilt

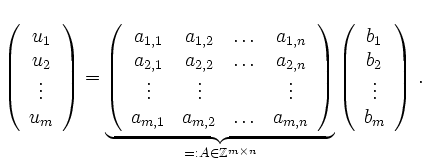
$\displaystyle \left ( \begin{array}{c} u_1\\ u_2 \\ \vdots\\ u_m \end{array} \r... ...n}} \left ( \begin{array}{c} b_1\\ b_2 \\ \vdots\\ b_m \end{array} \right) \,. $

Ein Basiswechsel in $ F$ entspricht der Multiplikation von $ A$ von rechts mit einer regulären Matrix aus $ {\mathbb{Z}}^{n\times n}$.

Ein Basiswechsel in $ U$ entspricht der Multiplikation von $ A$ von links mit einer regulären Matrix aus $ {\mathbb{Z}}^{m\times m}$.

Wählt man spezielle reguläre Matrizen obiger Art, so lassen sich folgende Umformungen von $ A$ durchführen:

Wegen des Euklidischen Algorithmus' kann man mit Hilfe dieser Umformungen $ A$ in die Form

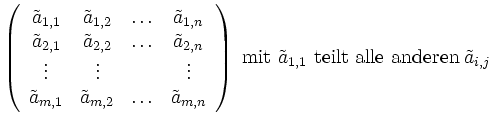
$\displaystyle \left ( \begin{array}{cccc} \tilde{a}_{1,1} & \tilde{a}_{1,2} & \... ...) \textrm{ mit } \tilde{a}_{1,1} \textrm{ teilt alle anderen } \tilde{a}_{i,j} $

bringen. Durch Abziehen der ersten Zeile und Spalte von den anderen bringt man $ A$ in die Form

$\displaystyle \left ( \begin{array}{cccc} \tilde{a}_{1,1} & 0 & \ldots & 0\\ % ... ...right) \textrm{ mit } \tilde{a}_{1,1} \textrm{ teilt alle Einträge von } B \,. $

Mit Induktion erhält man schließlich

$\displaystyle A \cong \left ( \begin{array}{ccccccc} % e_{1,1} & 0 & \ldots & 0... ...&0 \end{array} \right) \textrm{ mit } e_{i,i} \textrm{ teilt } e_{i+1,i+1} \,. $

Setzt man $ z_i=e_{i,i}$ für $ i\leq m$ und $ z_i=0$ für $ i>m$, dann erhält man die Behauptung.
[Zurück zur Aussage]
  automatisch erstellt am 3. 11. 2006