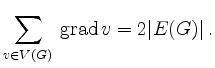Der Grad
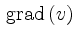 eines Knotens
eines Knotens 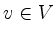 ist die Anzahl der Kanten von
ist die Anzahl der Kanten von 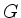 , die
, die 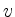 als Knoten
enthalten. Der Grad
als Knoten
enthalten. Der Grad
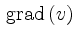 eines Knotens
eines Knotens 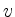 gibt also an, wie viele Nachbarn
gibt also an, wie viele Nachbarn 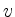 besitzt.
besitzt.
Es ist
und in jedem Graphen 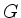 gilt:
gilt:
- (i)
- Die Anzahl der Knoten von
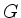 die einen ungeraden Grad haben ist gerade.
die einen ungeraden Grad haben ist gerade.
- (ii)
- Es gibt in
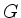 zwei Knoten von gleichem Grad.
zwei Knoten von gleichem Grad.
- (i)
- Es gilt die Gleichung
Damit die linke Seite eine gerade Zahl ergibt, muss die Anzahl der Knoten mit ungeradem Grad gerade sein.
- (ii)
- Die Aussage wird mit dem Schubfachprinzip bewiesen. Man setzt
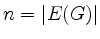 . Die Schubfächer sind mit
den möglichen Graden beschriftet. Wegen
. Die Schubfächer sind mit
den möglichen Graden beschriftet. Wegen
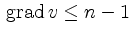 gibt es dann
gibt es dann 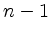 verschiedene
Schubfächer. Jeder Knoten wird nun in dem Schubfach abgelegt, der seinem Grad entspricht, d.h. Knoten im
gleichen Schubfächern haben den gleichen Grad. Da es zwar
verschiedene
Schubfächer. Jeder Knoten wird nun in dem Schubfach abgelegt, der seinem Grad entspricht, d.h. Knoten im
gleichen Schubfächern haben den gleichen Grad. Da es zwar 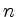 viele Knoten, jedoch nur
viele Knoten, jedoch nur 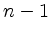 viele Schubfächer
gibt, ist mindestens ein Schubfach doppelt belegt.
viele Schubfächer
gibt, ist mindestens ein Schubfach doppelt belegt.
(Aus: Vorkurs Mathematik)
| |
automatisch erstellt
am 26. 2. 2007 |


![]() gilt:
gilt: