Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Lexikon: Erläuterung zu

Dreieck

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht
Ein Dreieck besteht aus drei nicht auf einer Geraden liegenden Punkten $ A,B,C$ und drei Seiten, den Verbindungsstrecken $ \overline{AB}, \overline{AC}$ und $ \overline{BC}$ der Punkte. Die Punkte $ A,B,C$ heißen Eckpunkte. Die Reihenfolge der Bezeichnungen wird in der Regel entgegen dem Uhrzeigersinn gewählt. Die Längen der Dreiecksseiten werden im Allgemeinen wie folgt benannt:

$\displaystyle a=\vert\overline{BC}\vert \ ; \ b=\vert\overline{AC}\vert \ \textrm{ und } \ c=\vert\overline{AC}\vert $

Die Winkel bei den Eckpunkten werden üblicherweise mit den ersten drei griechischen Kleinbuchstaben $ \alpha, \beta$ und $ \gamma$ bezeichnet. Dabei erhält der Winkel bei Punkt $ A$ die Bezeichnung $ \alpha$, bei $ B$ die Bezeichnung $ \beta$ und bei $ C$ heißt der Winkel $ \gamma$.

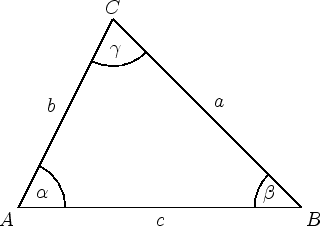
\includegraphics{geo_bild01}

Die Winkelsumme in jedem Dreieck beträgt $ 180^{\circ}$. Das heißt in einem beliebigen Dreieck gilt stets

$\displaystyle \alpha + \beta + \gamma = 180^{\circ} \,. $

Zum Beweis betrachtet man die folgende Skizze:

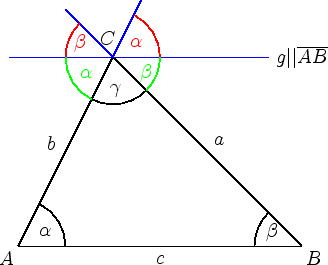
\includegraphics{geo_bild02}

Die horizontale blaue Linie ist parallel zu $ \overline{AB}$. Daher sind die rot eingezeichneten Winkel die Stufenwinkel zu den Winkeln $ \alpha$ und $ \beta$ des Dreiecks, und damit gleich groß wie diese Winkel. Die grün eingezeichneten Winkel sind die zu den Stufenwinkel gehörenden Wechselwinkel, die damit ebenfalls gleich groß wie die entsprechenden Winkel im Dreieck sind. Die Summe dieser Wechselwinkel und $ \gamma$ muss $ 180°$ ergeben. Es gilt also

$\displaystyle \alpha + \beta + \gamma= 180° \,. $

(Autor: Vorkurs Mathematik)
[Zurück zur Aussage]
  automatisch erstellt am 23. 10. 2007