Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Lexikon: Erläuterung zu

Tensorprodukt von Integrationsformeln

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Übersicht

Integrationsformeln für Rechteck-Gebiete

$\displaystyle Q = [a_1,b_1] \times \cdots \times [a_m,b_m] $

erhält man durch Bilden von Tensorprodukten eindimensionaler Quadraturformeln.

\includegraphics[width=0.5\linewidth]{Bild_Rechteck_Quadratur}

Sind die Formeln $ \sum_k w_{k,\nu} f(t_{k,\nu})$ zur Approximation von $ \int_{a_\nu}^{b_\nu} f$ exakt für Polynome vom Grad $ \le n_\nu$, so ist die Produktformel

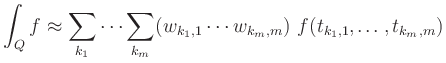
$\displaystyle \int_Q f \approx \sum_{k_1} \cdots \sum_{k_m} (w_{k_1,1}\cdots w_{k_m,m}) \ f(t_{k_1,1},\ldots,t_{k_m,m}) $

exakt für Polynome vom Koordinatengrad $ \le (n_1,\ldots,n_m)$.

Das Beweisprinzip wird für zwei Variable illustriert ($ m=2$). Seien dazu

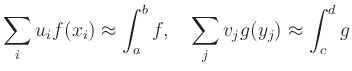
$\displaystyle \sum_i u_i f(x_i) \approx \int_a^b f,\quad \sum_j v_j g(y_j) \approx \int_c^d g $

die beiden univariaten Quadraturformeln. Dann hat die bivariate Formel die Form

$\displaystyle s = \sum_i u_i \left[ \sum_j v_j f(x_i,y_j) \right] \,. $

Ist $ f$ ein Polynom mit Koordinatengrad $ \le (n_1,n_2)$,

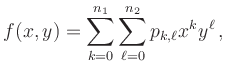
$\displaystyle f(x,y) = \sum_{k=0}^{n_1} \sum_{\ell=0}^{n_2} p_{k,\ell} x^k y^\ell \,, $

dann ist $ f(x_i,y)$ für festes $ x_i$ ein Polynom vom Grad $ \le n_2$ in $ y$. Deshalb stimmt der Ausdruck in eckigen Klammern mit dem Integral $ \int_c^d f(x_i,y)\,dy$ überein. Nach Vertauschen der Summe mit dem Integral ist dann

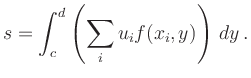
$\displaystyle s = \int_c^d \left( \sum_i u_i f(x_i,y) \right)\,dy \,. $

Wiederum stimmt die Summe wegen der Exaktheit mit dem entsprechenden Integral überein, und man erhält

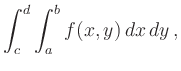
$\displaystyle \int_c^d \int_a^b f(x,y)\,dx\,dy \,, $

und damit den erwarteten Wert für $ s$.

[Zurück]
  automatisch erstellt am 17.  1. 2017