- a)
- Divergiert die Reihe
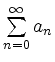 , so divergiert auch
die Folge
, so divergiert auch
die Folge 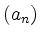 .
.
keine Angabe , wahr , falsch
- b)
- Ist die Funktion
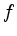 stetig auf
stetig auf
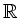 , so ist
sie auf jedem abgeschlossenen Intervall
, so ist
sie auf jedem abgeschlossenen Intervall
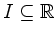 beschränkt.
beschränkt.
keine Angabe , wahr , falsch
- c)
- Es gibt unstetige Funktionen, die Lipschitz-stetig sind.
keine Angabe , wahr , falsch
- d)
- Die Funktionenfolge
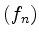 mit
mit
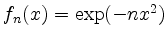 konvergiert
gleichmäßig auf
konvergiert
gleichmäßig auf
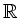 .
.
keine Angabe , wahr , falsch
- e)
- Konvergiert die Funktionenfolge
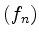 gleichmäßig auf
gleichmäßig auf
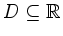 ,
dann konvergiert auch die Funktionenfolge
,
dann konvergiert auch die Funktionenfolge 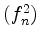 gleichmäßig auf
gleichmäßig auf 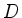 .
.
keine Angabe , wahr , falsch

