| a) |
Ein Punkt in 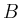 mit größtmöglichem mit größtmöglichem 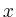 -Wert gibt den maximalen Gewinn. -Wert gibt den maximalen Gewinn. |
wahr , falsch |
|---|
| b) |
Ein Punkt in 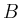 mit größtmöglichem mit größtmöglichem 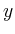 -Wert gibt den maximalen Gewinn. -Wert gibt den maximalen Gewinn. |
wahr , falsch |
|---|
| c) |
Verschiebt man die Gerade
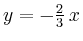 möglichst weit
parallel zur möglichst weit
parallel zur 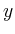 -Achse nach oben, solange noch ein Punkt aus -Achse nach oben, solange noch ein Punkt aus 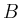 daraufliegt, so erhält man einen Punkt mit maximalem Gewinn.
daraufliegt, so erhält man einen Punkt mit maximalem Gewinn. |
wahr , falsch |
|---|
| d) |
Verschiebt man die Gerade
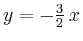 möglichst weit
parallel zur möglichst weit
parallel zur 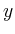 -Achse nach oben, solange noch ein Punkt aus -Achse nach oben, solange noch ein Punkt aus 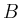 daraufliegt,
so erhält man einen Punkt mit maximalem Gewinn.
daraufliegt,
so erhält man einen Punkt mit maximalem Gewinn. |
wahr , falsch |
|---|
| e) |
Der größte Gewinn wird immer auf einem Eckpunkt von 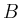 erzielt. erzielt. |
wahr , falsch |
|---|
| f) |
Lässt man auch nichtganzzahlige Werte von 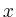 und und 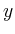 zu, so
wird der größte Gewinn immer auf einem Eckpunkt von zu, so
wird der größte Gewinn immer auf einem Eckpunkt von 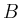 erzielt. erzielt. |
wahr , falsch |
|---|

