
Mathematik-Online-Aufgabensammlung: Lösungshinweis zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösungshinweis zu | |
Aufgabe 277: Konfidenzintervall (Wahlausgang) |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Ein Meinungsforschungsinstitut wird damit beauftragt, eine Umfrage
über den Ausgang eines ,,Bürgerentscheids ja/nein`` durchzuführen. Wie
viele zufällig ausgewählte Bürger müssen befragt werden, damit mit einem Konfidenzintervall der Länge
![]() für den empirischen Mittelwert für den Ausgang des Entscheids ein Konfidenzniveau von
für den empirischen Mittelwert für den Ausgang des Entscheids ein Konfidenzniveau von
![]() erreicht wird.
erreicht wird.
Mit
![]() setze man
setze man
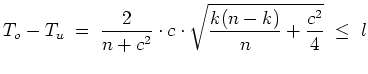
| automatisch erstellt am 7. 6. 2005 |