
Mathematik-Online-Aufgabensammlung: Lichtbrechung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lichtbrechung zu | |
Aufgabe 283: Lichtbrechung |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Wenn
![]() den Weg eines Lichtstrahls zwischen
den Weg eines Lichtstrahls zwischen
![]() und
und
![]() beschreibt, so bezeichne
beschreibt, so bezeichne
![]() die dafür benötigte Zeit.
Das Fermat-Prinzip besagt nun folgendes.
die dafür benötigte Zeit.
Das Fermat-Prinzip besagt nun folgendes.
Gibt man sich Randbedingungen
![]() und
und
![]() vor,
so minimiert der tatsächliche Weg des Lichts die Größe
vor,
so minimiert der tatsächliche Weg des Lichts die Größe
![]() .
.
Gibt man sich Randbedingungen
![]() und
und
![]() vor,
so minimiert der tatsächliche Weg des Lichts ebenfalls die Größe
vor,
so minimiert der tatsächliche Weg des Lichts ebenfalls die Größe
![]() ,
und zwar für jedes beliebig gewählte
,
und zwar für jedes beliebig gewählte
![]() .
.
Der Brechungsindex
![]() in einem lichtdurchlässigen Medium hänge
nur von der Höhe ab. Hierbei ist
in einem lichtdurchlässigen Medium hänge
nur von der Höhe ab. Hierbei ist
![]() die Vakuumslichtgeschwindigkeit, und
die Vakuumslichtgeschwindigkeit, und
![]() die Lichtgeschwindigkeit in Höhe
die Lichtgeschwindigkeit in Höhe
![]() .
.
Gib die Euler-Lagrange-Gleichung an.
Für
![]() berechne man jeweils
berechne man jeweils
Da
![]() nicht explizit von
nicht explizit von
![]() abhängt,
muß die Euler-Lagrange Bedingung
abhängt,
muß die Euler-Lagrange Bedingung
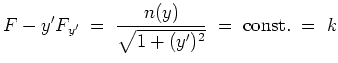
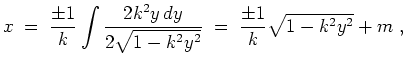
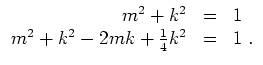
![\includegraphics[width=6cm]{s1.eps}](/inhalt/loesung/loesung278/img13.png)
Die Randbedingung (1) direkt in die Differentialgleichung eingesetzt, ergibt
![]() . Mit
. Mit
![]() wird schließlich
wird schließlich
![]() . Der Ansatz
. Der Ansatz
![]() liefert dann
liefert dann
![]() . Das Licht kommt also bei
. Das Licht kommt also bei
![]() zum Stillstand.
zum Stillstand.
![\includegraphics[width=6cm]{s11.eps}](/inhalt/loesung/loesung278/img20.png)
Bemerkung:
In der Atmosphäre wird Licht allerdings nicht entlang von Kreisbögen
gebeugt, da ein anderer Brechungsindex vorliegt:
Luft hat (auf Meereshöhe) den Brechungsindex von etwa
![]() .
Da sich der Luftdruck etwa alle
.
Da sich der Luftdruck etwa alle
![]() halbiert, gilt für
den Brechungsindex in etwa
halbiert, gilt für
den Brechungsindex in etwa
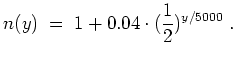
| automatisch erstellt am 7. 6. 2005 |