Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösungshinweis zu

Aufgabe 284: durchhängendes Seil

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Ein Seil der Länge $ \mbox{$2.35 \text{m}$}$ werde zwischen zwei gleichhohen Befestigungspunkten aufgehängt, welche einen Abstand von $ \mbox{$2 \text{m}$}$ haben. Gebe eine Funktion $ \mbox{$y$}$ an, die die Seilhöhe zwischen den Befestigungspunkten beschreibt. Wie tief hängt das Seil durch?

Für die Rechung verwende man $ \mbox{$2.35\approx \exp(1) - \exp(-1)$}$.

Wähle $ \mbox{$x_0 = -1, x_1 = 1, y_0 = 0, y_1 = 0$}$. Die Höhe des Schwerpunkts

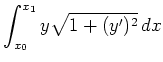
$ \mbox{$\displaystyle \int_{x_0}^{x_1} y \sqrt{1+(y')^2}\, dx $}$
soll minimiert werden, bei konstanter Seillänge
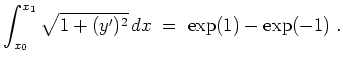
$ \mbox{$\displaystyle \int_{x_0}^{x_1} \sqrt{1+(y')^2}\, dx \; =\; \exp(1) - \exp(-1)\; . $}$

(Autoren: Künzer/Meister/Nebe)
[Zurück zur Aufgabe]
  automatisch erstellt am 7.  6. 2005