Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösungshinweis zu

Aufgabe 286: Verkehrsdichte, lineare partielle Differentialgleichung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Sei die Verkehrsdichte auf einer Straße durch $ u(x,t)$ gegeben, d.h. $ u(x,t)$ ist die Zahl der Autos an der Stelle $ x$ zum Zeitpunkt $ t$ zwischen $ x$ und $ x + dx$, geteilt durch $ dx$.

Sei der Verkehrsfluß durch $ F(x,t)$ beschrieben. Der Wert $ F(x,t)$ ist hierbei die Zahl der Autos, die die Stelle $ x$ im Zeitraum von $ t$ bis $ t + dt$ in positiver Richtung passieren.

Betrachten wir das Streckenelement $ [x,x+dx]$ zum Zeitpunkt $ t$. Fluß und Dichte hängen über

$\displaystyle (u(x,t+dt) - u(x,t))dx\; =\; - (F(u(x+dx,t)) - F(u(x,t))) dt $

zusammen, da die Änderung der Verkehrsdichte der Zahl der in das Streckenelement bei $ x$ einfahrenden Autos, minus der bei $ x + dx$ ausfahrenden Autos gegeben ist. Also

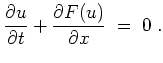
$\displaystyle \frac{\partial u}{\partial t} + \frac{\partial F(u)}{\partial x} \; = \; 0\; . $

(i)
Sei der Verkehrsfluß $ F(x,t)$ nur von $ u$ abhängig - die Geschwindigkeit eines Autos ist durch den Abstand zum Vordermann bestimmt. Wir setzen also $ F(x,t) = F(u(x,t)) = 1 - u$ an. D.h. ist die Verkehrsdichte Null, so fahren alle Autos mit Geschwindigkeit $ 1$, ist die Verkehrsdichte auf $ 1$ angeschwollen, so kommt der Verkehr zum Erliegen. Ist die Verkehrsdichte $ >1$, so kommt es zu Auffahrunfällen.

(ii)
Sei nun der Verkehrfluß noch von der sich den Orten $ x = 2\pi\mathbb{Z}$ befindlichen Polizeistationen abhängig - je näher an $ x = 0$, desto mehr wird auf den zu geringen Abstand zum Vordermann mit Geschwindigkeitsreduktion reagiert. Sei demgemäß $ F(x,t) = F(u(x,t)) = 1 - (1 + a\cos(x)) u$ mit $ a\in [0,1)$.

Gib die allgemeine Lösung der Differentialgleichung in den Fällen (i, ii) an.

Sei nun als Randbedingung $ u(x,0) = 1/2$ vorausgesetzt. Gib die Funktion $ u(x,t)$ in beiden Fällen an.

Im Fall (i) lautet die Differentialgleichung $ \mbox{$u_t - u_x = 0$}$.

Im Fall (ii) lautet die Differentialgleichung $ \mbox{$u_t + a\sin(x) u - (1+a\cos(x)) u_x = 0$}$.

Fall (i) ergibt sich also für $ \mbox{$a = 0$}$ aus Fall (ii).

(Autoren: Künzer/Meister/Nebe)
[Zurück zur Aufgabe]
  automatisch erstellt am 7.  6. 2005