
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 854: Explizite Darstellung von Funktionswerten einer rekursiv definierten Funktion |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Die Funktion
![]() sei rekursiv definiert durch die Anfangsbedingungen
sei rekursiv definiert durch die Anfangsbedingungen
![]() ,
,
![]() , und durch die Rekursionsgleichung
, und durch die Rekursionsgleichung
Die ersten Werte der Funktion
![]() lauten
lauten
![]() . Daraus kann man die Vermutung
. Daraus kann man die Vermutung
![]() ableiten. Wir beweisen diese Formel durch Induktion.
ableiten. Wir beweisen diese Formel durch Induktion.
Induktionsanfang:
![]() .
.
Induktionsschritt: Wir nehmen an, die Formel stimmt für alle
![]() mit
mit
![]() . Wir müssen zeigen, daß sie
auch für
. Wir müssen zeigen, daß sie
auch für
![]() gilt.
gilt.
Fall
![]() . Hier gilt die Formel, es ist
. Hier gilt die Formel, es ist
![]() . (Diesen Fall kann man auch als Teil
des Induktionsanfangs sehen.)
. (Diesen Fall kann man auch als Teil
des Induktionsanfangs sehen.)
Fall
![]() . Nun haben wir nach Induktion die Gültigkeit der Formel für
. Nun haben wir nach Induktion die Gültigkeit der Formel für
![]() und
und
![]() zur Verfügung.
Wir erhalten
zur Verfügung.
Wir erhalten
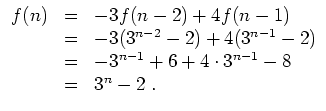
| automatisch erstellt am 7. 6. 2005 |