Mathematik-Online-Aufgabensammlung: Lösung zu: Aufgabe 860: Grenzwert einer Folge

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Aufgabensammlung: Lösung zu
	Aufgabe 860: Grenzwert einer Folge

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Sei $\mbox{$a_n := 1\cdot n^{-2} + 2\cdot n^{-2} + \cdots + n\cdot n^{-2}$}$ . Untersuche $\mbox{$(a_n)_{n\geq 1}$}$ auf Konvergenz und bestimme gegebenenfalls den Grenzwert.

Es wird

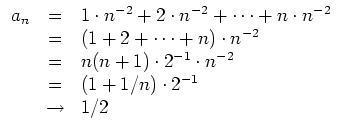
$\mbox{$\displaystyle \begin{array}{rcl} a_n & = & 1\cdot n^{-2} + 2\cdot n^{... ...ot 2^{-1}\cdot n^{-2}\\ & = & (1+1/n)\cdot 2^{-1}\\ &\to& 1/2 \end{array}$}$

für $\mbox{$n\to\infty$}$ .

Wir merken an, daß man die Summe nicht mit den Grenzwertregeln auflösen kann, da die Zahl der Summanden von $\mbox{$n$}$ abhängt.

(Autoren: Künzer/Martin/Nebe)

[Zurück zur Aufgabe]

automatisch erstellt am 7. 6. 2005