Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 868: Konvergenz von Reihen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Untersuche jeweils die Reihe $ \mbox{$\sum_{n=1}^\infty a_n$}$ auf Konvergenz. Berechne von wenigstens einer konvergenten Reihe den Grenzwert.

  1. $ \mbox{$a_n = 1/{3n\choose n}$}$.
  2. $ \mbox{$a_n = 1/\sqrt{n^2+1}$}$.
  3. $ \mbox{$a_n = 2^{((-1)^n-2)n}$}$.
  4. $ \mbox{$a_n = z^n/n^\alpha$}$, wobei $ \mbox{$z\in\mathbb{C}$}$ und $ \mbox{$\alpha\in(0,1]$}$.

  1. Wir verwenden zunächst das Quotientenkriterium. Es wird
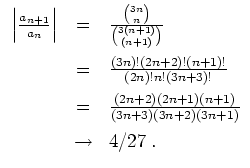
    $ \mbox{$\displaystyle \begin{array}{rcl} \left\vert\frac{a_{n+1}}{a_n}\right\v... ...1)(n+1)}{(3n+3)(3n+2)(3n+1)}\vspace*{2mm}\\ &\to& 4/27\; . \\ \end{array}$}$
    Also konvergiert die Reihe absolut.

    Alternativ kann man auch das Wurzelkriterium gebrauchen. Zunächst bemerken wir, daß aus der schwachen Stirlingschen Formel $ \mbox{$\sqrt[n]{n!}/n\to 1/e$}$ durch Substitution von $ \mbox{$3n$}$ für $ \mbox{$n$}$ und Potenzieren mit $ \mbox{$3$}$ folgt, daß $ \mbox{$\sqrt[n]{(3n)!}/(3n)^3\to 1/e^3$}$. Es wird

    $ \mbox{$\displaystyle \begin{array}{rcl} \lim_{n\to\infty} \sqrt[n]{\vert a_n\... ... \cdot \frac{4}{27} \vspace*{2mm}\\ & = & \frac{4}{27}\; . \\ \end{array}$}$
  2. Wäre die Reihe konvergent, so folgte mit dem Majorantenkriterium wegen $ \mbox{$1/\sqrt{n^2+1} \geq 1/(2n)$}$, daß die Reihe $ \mbox{$\sum_n 1/(2n)$}$ konvergierte. Die harmonische Reihe ist aber divergent, womit die Annahme zu einem Widerspruch geführt ist. Damit ist die ursprüngliche Reihe als divergent nachgewiesen.

  3. Mit dem Wurzelkriterium folgt wegen
    $ \mbox{$\displaystyle \overline {\lim}_{n\to\infty} \sqrt[n]{\vert a_n\vert} \; =\; \overline {\lim}_{n\to\infty} 2^{(-1)^n - 2} \; = \; 1/2\, , $}$
    daß die Reihe konvergiert.

    In der Tat ist mit der geometrischen Reihe

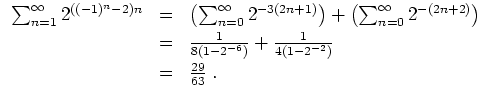
    $ \mbox{$\displaystyle \begin{array}{rcl} \sum_{n = 1}^\infty 2^{((-1)^n - 2)n}... ...ac{1}{4(1-2^{-2})} \vspace*{1mm}\\ & = & \frac{29}{63}\; . \\ \end{array}$}$

    Man kann die Konvergenz der Reihe auch mit dem Majorantenkriterium nachweisen. Es ist nämlich $ \mbox{$\vert a_n\vert\leq 2^{(1-2)n}=2^{-n}$}$, und die geometrische Reihe $ \mbox{$\sum_n 2^{-n}$}$ konvergiert.

    Das Quotientenkriterium versagt hier, da der fragliche Limes superior gleich $ \mbox{$+\infty$}$, und der fragliche Limes inferior gleich $ \mbox{$0$}$ ist.

  4. Das Wurzelkriterium liefert
    $ \mbox{$\displaystyle \begin{array}{rcl} \overline {\lim}_{n\to\infty}\sqrt[n]... ...ac{\vert z\vert}{\exp(\alpha(\log n)/n)}\\ &=& \vert z\vert\; . \end{array}$}$
    Also konvergiert die Reihe (sogar absolut) für $ \mbox{$\vert z\vert<1$}$ und divergiert für $ \mbox{$\vert z\vert>1$}$.

    Im Falle $ \mbox{$\vert z\vert=1$}$ mit $ \mbox{$z\ne 1$}$ wollen wir das Dirichletkriterium verwenden mit $ \mbox{$x_n:=z^n$}$ und $ \mbox{$y_n:=1/n^\alpha$}$, indem wir zeigen, daß die Partialsummenfolge $ \mbox{$(\sum_{n=1}^k x_n)_k$}$ beschränkt ist, und daß die Folge $ \mbox{$(y_n)_n$}$ eine monotone Nullfolge ist. Es wird

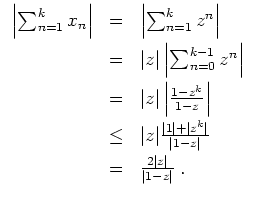
    $ \mbox{$\displaystyle \begin{array}{rcl} \left\vert\sum_{n=1}^k x_n\right\vert... ...rt}\vspace*{1mm}\\ &=& \frac{2\vert z\vert}{\vert 1-z\vert}\; . \end{array}$}$
    Damit ist die Partialsummenfolge beschränkt. Wegen $ \mbox{$\alpha\in(0,1]$}$ ist $ \mbox{$(y_n)_n=(1/n^\alpha)_n$}$ eine monotone Nullfolge. Also konvergiert die Reihe $ \mbox{$\sum_n a_n=\sum_n x_ny_n$}$ im Falle $ \mbox{$\vert z\vert=1$}$ mit $ \mbox{$z\ne 1$}$.

    Für $ \mbox{$z=1$}$ betrachtet man $ \mbox{$1/n^\alpha\geq 1/n$}$. Nach dem Majorantenkriterium folgt aus der Divergenz der harmonischen Reihe $ \mbox{$\sum_n 1/n$}$ die Divergenz der Reihe $ \mbox{$\sum_n a_n=\sum_n 1/n^\alpha$}$.

(Autoren: Künzer/Martin/Nebe)
[Zurück zur Aufgabe]
  automatisch erstellt am 7.  6. 2005