Mathematik-Online-Aufgabensammlung: Lösung zu: Aufgabe 869: Konvergenz von Reihen

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Aufgabensammlung: Lösung zu
	Aufgabe 869: Konvergenz von Reihen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Für welche $\mbox{$\alpha\in\mathbb{R}_{>0}$}$ konvergiert jeweils die Reihe $\mbox{$\sum_{n\geq n_0} a_n$}$ ( $\mbox{$n_0$}$ geeignet gewählt)?

$\mbox{$a_n=\frac{1}{n^\alpha}$}$ .
$\mbox{$a_n=\frac{1}{n (\log n)^\alpha}$}$ .
$\mbox{$a_n=\frac{1}{n (\log n) (\log\log n)^\alpha}$}$ .
$\mbox{$a_n=\frac{1}{n (\log n) (\log\log n) (\log\log\log n)^\alpha}$}$ .

In allen vier Teilaufgaben ist die Folge $\mbox{$a_n$}$ eine monoton fallende Folge ab einem geeigneten $\mbox{$n_0$}$ . Nach dem Cauchyschen Verdichtungskriterium können wir jeweils die Reihe $\mbox{$\sum_n 2^n a_{2^n}$}$ betrachten.

Es ist $\mbox{$2^n a_{2^n}=\frac{2^n}{(2^n)^\alpha}=(2^{1-\alpha})^n$}$ . Die geometrische Reihe $\mbox{$\sum_n (2^{1-\alpha})^n$}$ konvergiert für $\mbox{$\alpha>1$}$ und divergiert für $\mbox{$\alpha\leq 1$}$ . Also gilt dies auch für die Reihe $\mbox{$\sum_n a_n$}$ .
Es ist $\mbox{$2^n a_{2^n}=\frac{2^n}{2^n(\log(2^n))^\alpha}=\frac{1}{(\log 2)^\alpha n^\alpha}$}$ . Nach Teil 1 konvergiert die Reihe $\mbox{$\sum_n \frac{1}{n^\alpha}$}$ für $\mbox{$\alpha>1$}$ und divergiert für $\mbox{$\alpha\leq 1$}$ . Also gilt dies auch für die Reihe $\mbox{$\sum_n a_n$}$ .
Es wird
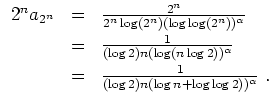
$\mbox{$\displaystyle \begin{array}{rcl} 2^n a_{2^n} &=& \frac{2^n}{2^n\log(2^... ...1mm}\\ &=& \frac{1}{(\log 2) n (\log n+\log\log 2))^\alpha}\; . \end{array}$}$
Ferner gilt $\mbox{$\log\log 2\leq 0$}$ und $\mbox{$\log\log 2\geq -\frac{1}{2}\log n$}$ für $\mbox{$n\geq 3$}$ . Also können wir diesenfalls den Summanden $\mbox{$2^n a_{2^n}$}$ abschätzen durch
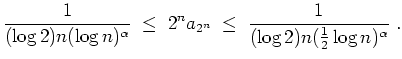
$\mbox{$\displaystyle \frac{1}{(\log 2) n (\log n)^\alpha} \;\leq\; 2^n a_{2^n} \;\leq\; \frac{1}{(\log 2) n (\frac{1}{2}\log n)^\alpha}\; . $}$
Nach dem Majorantenkriterium und Teil 2 erhalten wir Konvergenz für $\mbox{$\alpha>1$}$ und Divergenz für $\mbox{$\alpha\leq 1$}$ .
Es wird
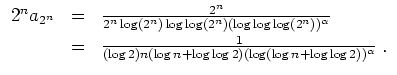
$\mbox{$\displaystyle \begin{array}{rcl} 2^n a_{2^n} &=& \frac{2^n}{2^n\log(2^... ...) n (\log n+\log\log 2) (\log(\log n+\log\log 2))^\alpha}\; .\\ \end{array}$}$
Ferner gilt $\mbox{$\log\log 2\leq 0$}$ , $\mbox{$\log\log 2\geq -\frac{1}{2}\log n$}$ für $\mbox{$n\geq 3$}$ und $\mbox{$-\log 2\geq -\frac{1}{2}\log\log n$}$ für $\mbox{$n\geq 55$}$ . Also können wir diesenfalls den Summanden $\mbox{$2^n a_{2^n}$}$ abschätzen durch
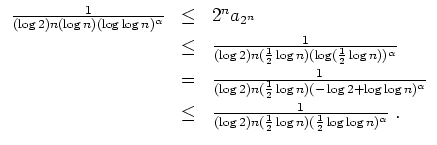
$\mbox{$\displaystyle \begin{array}{rcl} \frac{1}{(\log 2) n (\log n) (\log\lo... ... 2) n (\frac{1}{2}\log n)(\frac{1}{2}\log\log n)^\alpha}\; . \\ \end{array}$}$
Nach dem Majorantenkriterium und Teil 2 erhalten wir Konvergenz für $\mbox{$\alpha>1$}$ und Divergenz für $\mbox{$\alpha\leq 1$}$ .

(Später mit Integralkriterium kürzer lösbar.)

(Autoren: Künzer/Martin/Nebe)

[Zurück zur Aufgabe]

automatisch erstellt am 7. 6. 2005