
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 871: Reihendarstellung rationaler Funktionen |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
Man überprüfe die Identität
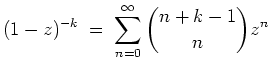
Wir haben nachzuprüfen, daß
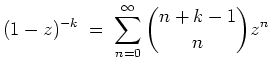
Zunächst einmal halten wir fest, daß die Potenzreihe auf der rechten Seite der Identität den Konvergenzradius
![]() besitzt.
besitzt.
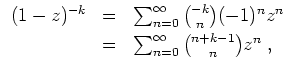
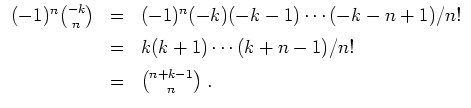
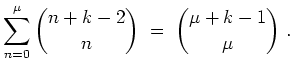
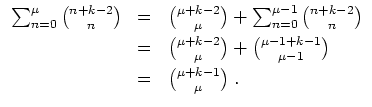
Nun zur Aufgabe. Für
![]() folgt die Identität wegen
folgt die Identität wegen
![]() aus der geometrischen Reihe.
aus der geometrischen Reihe.
Sei
![]() , und sei die Identität als gültig angenommen für
, und sei die Identität als gültig angenommen für
![]() . Mittels Cauchyprodukt wird
. Mittels Cauchyprodukt wird
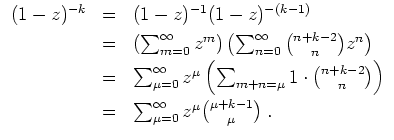
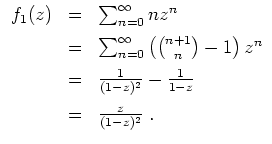
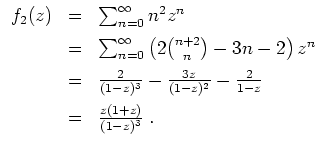
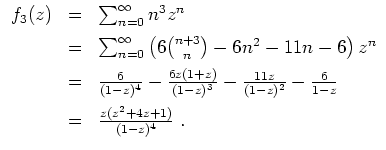
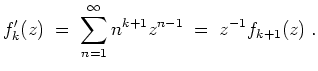
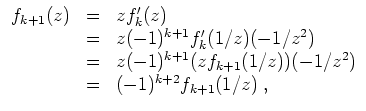
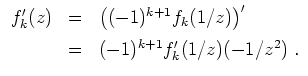
| automatisch erstellt am 7. 6. 2005 |