Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 880: Taylorentwicklung der Tangens-Funktion

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Bestimme die Taylorentwicklung von $ \mbox{$\tan x$}$ um $ \mbox{$x_0 = 0$}$ mit $ \mbox{$n = 5$}$ .

Liefert eine Abschätzung des Restglieds hier Schranken für eine polynomiale Approximation auf $ \mbox{$(-\pi/2,+\pi/2)$}$  ?

Wir bilden zunächst einmal die iterierten Ableitungen.

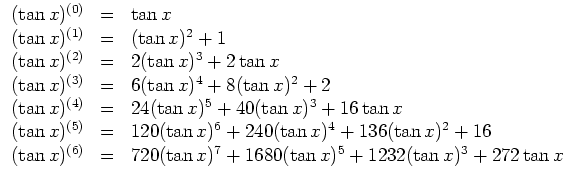
$ \mbox{$\displaystyle \begin{array}{rcl} (\tan x)^{(0)} & = & \tan x \\ (\ta... ... 720(\tan x)^7 + 1680(\tan x)^5 + 1232(\tan x)^3 + 272\tan x \\ \end{array}$}$
Mit $ \mbox{$\tan 0 = 0$}$ erhalten wir die Taylorentwicklung für $ \mbox{$n = 5$}$
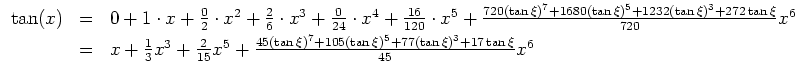
$ \mbox{$\displaystyle \begin{array}{rcl} \tan(x) & = & 0 + 1\cdot x + \frac{0... ...\xi)^7 + 105(\tan\xi)^5 + 77(\tan\xi)^3 + 17\tan\xi}{45} x^6 \\ \end{array}$}$
für ein $ \mbox{$\xi$}$ zwischen $ \mbox{$0$}$ und $ \mbox{$x$}$.

Wir bemerken noch, daß nur die Koeffizienten mit ungeradem Index in der Taylorentwicklung um $ \mbox{$0$}$ nicht verschwinden, da es sich bei $ \mbox{$\tan x$}$ um eine ungerade Funktion handelt.

Im Restglied geht $ \mbox{$45(\tan\xi)^7 + 105(\tan\xi)^5 + 77(\tan\xi)^3 + 17\tan\xi$}$ gegen $ \mbox{$+\infty$}$ für $ \mbox{$\xi\to\pi/2$}$. Da wir für $ \mbox{$x\to\pi/2$}$ auch nicht ausschließen können, daß sich $ \mbox{$\xi$}$ nahe bei $ \mbox{$\pi/2$}$ befindet, erhalten wir über das Restglied keine Schranken für die Approximation von $ \mbox{$\tan x$}$ durch $ \mbox{$x + \frac{1}{3} x^3 + \frac{2}{15} x^5$}$. Da $ \mbox{$\tan x$}$ im Gegensatz zu diesem Polynom auf $ \mbox{$(-\pi/2,+\pi/2)$}$ unbeschränkt ist, kann eine solche Schranke auch nicht existieren.

(Autoren: Künzer/Martin/Nebe)
[Aufgabe]
  automatisch erstellt am 17. 12. 2007