
Mathematik-Online-Aufgabensammlung: Lösung zu

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Aufgabensammlung: Lösung zu | |
Aufgabe 886: Konvergenz von Reihen |
| A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
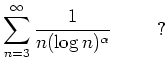
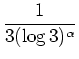 differierende obere und
untere Schranken für den Wert der Summe an.
differierende obere und
untere Schranken für den Wert der Summe an.
Sei
![]() , sei
, sei
![]() . Etwas allgemeiner als in (1), für welche reelle
. Etwas allgemeiner als in (1), für welche reelle
![]() konvergiert die Reihe
konvergiert die Reihe
![$ \mbox{$\displaystyle
\sum_{n = N}^\infty\frac{1}{(\log^{[m]} n)^\alpha\cdot \prod_{\nu = 0}^{m-1} \log^{[\nu]} n}\hspace*{1cm}{\mbox{?}}
$}$](/inhalt/aufgabe/aufgabe886/img11.png)
Wir erhalten dann mit der Substitution
![]() und
und
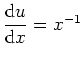
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\displaystyle\int _3^\infty\frac{{\mb...
...m_{t\to\infty} [(1-\alpha)^{-1} u^{1-\alpha}]_{\log 3}^t\; , \\
\end{array}$}$](/inhalt/loesung/loesung499/img5.png)
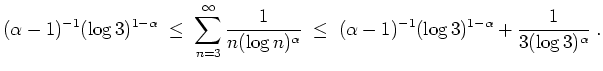
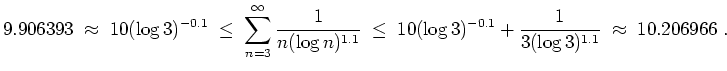
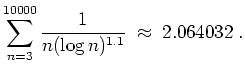
Wir erhalten dann mit der Substitution
![]() und
und
![$ \mbox{${\displaystyle\frac{{\mbox{d}}u}{{\mbox{d}}x}} = \prod_{\nu = 0}^{m-1} (\log^{[\nu]} x)^{-1}$}$](/inhalt/loesung/loesung499/img15.png)
![$ \mbox{$\displaystyle
\begin{array}{rcl}
\displaystyle\int _N^\infty\frac{{\mb...
...o\infty} [(1-\alpha)^{-1} u^{1-\alpha}]_{\log^{[m]} N}^t\; , \\
\end{array}$}$](/inhalt/loesung/loesung499/img16.png)
![$ \mbox{$\displaystyle
(\alpha-1)^{-1}(\log^{[m]} N)^{1-\alpha}
\;\leq\;\sum_{n...
...frac{1}{(\log^{[m]} N)^\alpha\cdot \prod_{\nu = 0}^{m-1} \log^{[\nu]} N}\; .
$}$](/inhalt/loesung/loesung499/img18.png)
Skizze von
![]() .
.
![\includegraphics[width = 10cm]{s1_log3.eps}](/inhalt/loesung/loesung499/img20.png)
| automatisch erstellt am 7. 6. 2005 |