Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 892: Harmonischer Oszillator mit Luftreibung

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Ein in zwei Federn eingespannter Körper genügt unter Berücksichtigung des Luftwiderstandes der Bewegungsgleichung

$ \mbox{$\displaystyle m\ddot{x} + Dx + R\dot{x}\vert\dot{x}\vert \;=\; 0 \;. $}$
Dabei ist $ \mbox{$x=x(t)$}$ der Ort des Oszillators zum Zeitpunkt $ \mbox{$t$}$, $ \mbox{$m$}$ die Masse des Körpers, $ \mbox{$D$}$ die Federkonstante, und $ \mbox{$R$}$ eine von der Form und Größe des Körpers abhängige Konstante. Der Gleichgewichtspunkt ist bei $ \mbox{$x=0$}$.

Seien $ \mbox{$x(0) = x_0>0$}$ und $ \mbox{$\dot x(0) = 0$}$. Bestimme die Geschwindigkeit $ \mbox{$\dot{x}$}$ beim ersten Durchgang des Oszillators durch den Gleichgewichtspunkt.

Es handelt sich um eine autonome Gleichung. Wir setzen $ \mbox{$\dot{x}=v(x)$}$, d.h. $ \mbox{$v$}$ gibt die Geschwindigkeit in Abhängigkeit des Ortes an.

Dies führt zur Gleichung

$ \mbox{$\displaystyle 0 \; =\; mvv' + Dx - Rv^2\; , $}$
also zu
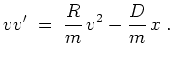
$ \mbox{$\displaystyle vv' \;=\; \frac{R}{m}\, v^2 - \frac{D}{m}\,x\;. $}$
Diese Gleichung für $ \mbox{$v$}$ ist eine Bernoullische Gleichung mit Exponent $ \mbox{$\alpha=-1$}$. Die Substitution $ \mbox{$\eta=v^2$}$ führt zu
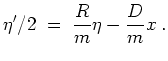
$ \mbox{$\displaystyle \eta'/2 \;=\; \frac{R}{m}\eta - \frac{D}{m} x\;. $}$
Dies ist eine inhomogene Gleichung.

Die allgemeine Lösung der zugehörigen homogenen Gleichung $ \mbox{$\eta'=\frac{2R}{m}\eta$}$ ist $ \mbox{$\eta = c\exp(2Rx/m)$}$ mit einer Konstanten $ \mbox{$c\in\mathbb{R}$}$. Eine partikuläre Lösung für die inhomogene Gleichung findet man durch Variation der Konstanten, also durch den Ansatz $ \mbox{$\eta=c(x)\exp(2Rx/m)$}$. Dies führt auf

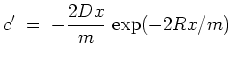
$ \mbox{$\displaystyle c' \;=\; -\frac{2Dx}{m}\,\exp(-2Rx/m) $}$
und also auf
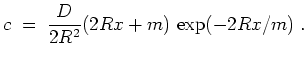
$ \mbox{$\displaystyle c \;=\; \frac{D}{2R^2}(2Rx+m)\,\exp(-2Rx/m)\; . $}$
Die allgemeine Lösung für $ \mbox{$\eta$}$ ist folglich
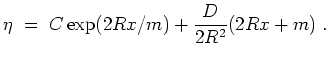
$ \mbox{$\displaystyle \eta \;=\; C\exp(2Rx/m) + \frac{D}{2R^2}(2Rx+m) \; . $}$
mit einer Konstanten $ \mbox{$C\in\mathbb{R}$}$. Somit ist aus physikalischen Gründen
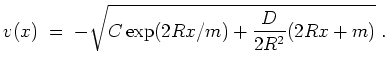
$ \mbox{$\displaystyle v(x) \; = \; -\sqrt{C\exp(2Rx/m) + \frac{D}{2R^2}(2Rx+m)}\; . $}$
negativ, und also
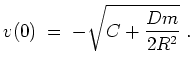
$ \mbox{$\displaystyle v(0) \; = \; -\sqrt{C + \frac{Dm}{2R^2}}\; . $}$
Es bleibt uns, die Konstante $ \mbox{$C$}$ zu bestimmen. Es sollte
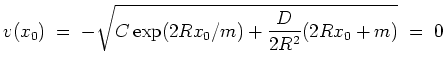
$ \mbox{$\displaystyle v(x_0) \; =\; -\sqrt{C\exp(2Rx_0/m) + \frac{D}{2R^2}(2Rx_0+m)} \; =\; 0 $}$
sein, d.h.
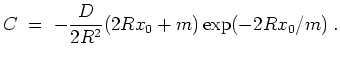
$ \mbox{$\displaystyle C\; =\; -\frac{D}{2R^2} (2Rx_0+m)\exp(-2Rx_0/m)\; . $}$

Skizze des Verlaufs von $ \mbox{$x(t)$}$ im Falle $ \mbox{$m=1$}$, $ \mbox{$D=1$}$ und $ \mbox{$R=1$}$ für einige Anfangswerte.

\includegraphics[width=10cm]{s1_osz.eps}
(Autoren: Künzer/Martin/Nebe)
[Zurück zur Aufgabe]
  automatisch erstellt am 7.  6. 2005