Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Hinweis zu

Aufgabe 894: Magnetischer Schwingkreis

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Wir schließen an eine Spannungsquelle mit Spannung $ \mbox{$U(t)$}$ seriell eine Spule mit Induktivität $ \mbox{$L>0$}$, einen Kondensator mit Kapazität $ \mbox{$C>0$}$ und einen Widerstand mit Widerstand $ \mbox{$2\sqrt{L/C}> R >0$}$ an. Für die Stromstärke $ \mbox{$I$}$ gilt dann

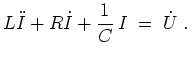
$ \mbox{$\displaystyle L\ddot{I} + R\dot{I}+{\displaystyle\frac{1}{C}}\,I \;=\; \dot{U} \;. $}$
Wir legen eine Wechselspannung $ \mbox{$U(t)=U_0\sin(\omega t)$}$ mit Frequenz $ \mbox{$\omega>0$}$ an.

(1)
Bestimme die allgemeine Lösung für die Stromstärke $ \mbox{$I(t)$}$.
(2)
Sei $ \mbox{$I_\infty(t)$}$ die Lösung mit konstanter Amplitude. Bestimme die Resonanzfrequenz $ \mbox{$\omega$}$; d.h. diejenige Frequenz $ \mbox{$\omega$}$, für die diese Amplitude maximal wird. Bestimme auch diese maximale Amplitude.

Es ist günstig, als Grundlösungen komplexe Exponentialfunktionen zu verwenden, und erst am Schluß auszunützen, daß der Realteil einer komplexen Lösung einer reellen Differentialgleichung wieder eine Lösung darstellt.

Zerlege hierzu auch die Inhomogenität, d.h. die angelegte Spannung, in komplexe Exponentialfunktionen.

(Autoren: Künzer/Martin/Nebe)
[Zurück zur Aufgabe]
  automatisch erstellt am 7.  6. 2005