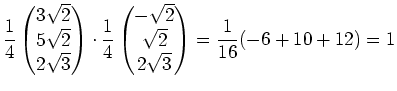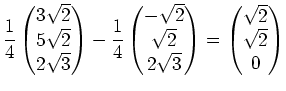Ein spurgebundenes Fahrzeug (Eisenbahn, Transrapid, etc.) übt momentan eine
Antriebskraft vom Betrag 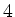 aus und bewegt sich dabei auf Schienen, die in
Richtung
aus und bewegt sich dabei auf Schienen, die in
Richtung
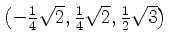 verlegt sind. Zusätzlich wirkt auf das Fahrzeug die Windkraft
verlegt sind. Zusätzlich wirkt auf das Fahrzeug die Windkraft
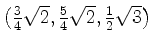 .
.
- a)
- Wie groß ist die Gesamtkraft in Fahrtrichtung?
- b)
- Wie groß ist die vom Wind erzeugte Querkraft auf die Schiene (die Kraft, die senkrecht zur
Schiene in der horizontalen Ebene, die von
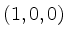 und
und 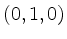 aufgespannt
wird, wirkt)?
aufgespannt
wird, wirkt)?
In dieser Aufgabe muss ein Vektor, nämlich der Vektor der Windkraft, in seine
Anteile nach verschiedenen Richtungen zerlegt werden. Zunächst erhält man den
Anteil in Fahrtrichtung, indem man den Vektor mit dem normierten
Richtungsvektor der Fahrtrichtung skalar multipliziert:
Damit muss man also den normierten Richtungsvektor einmal zur Antriebskraft
addieren, um die Gesamtkraft zu bekommen. Also ist die Gesamtkraft in
Fahrtrichtung
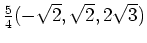 . Der restliche
Anteil wirkt senkrecht zur Fahrtrichtung, ist also Querkraft. Wir bekommen
sie, indem wir den Fahrtrichtungsanteil von der Windkraft abziehen und
erhalten für die Querkraft:
. Der restliche
Anteil wirkt senkrecht zur Fahrtrichtung, ist also Querkraft. Wir bekommen
sie, indem wir den Fahrtrichtungsanteil von der Windkraft abziehen und
erhalten für die Querkraft:
Da dieser Rest schon in der geforderten Ebene liegt, sind wir fertig.
(Ackermann/Poppitz)
| |
automatisch erstellt
am 19. 12. 2005 |