Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1129: Orthonormalsystem und Orthonormalbasis

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Ausgehend von den Vektoren $ v_1=(1,1,0,0)$, $ v_2=(0,2,0,1)$ sowie $ v_3=(-1,3,1,-1)$ sind für $ k=1,2,3$ die Vektoren

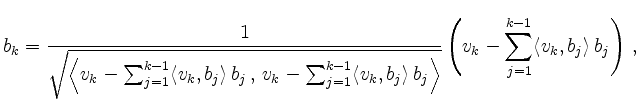
$\displaystyle b_k=\frac{1}{\sqrt{\left\langle v_k-\sum_{j=1}^{k-1}\langle v_k,b... ...right\rangle}}\left(v_k-\sum_{j=1}^{k-1}\langle v_k,b_j\rangle\,b_j\right) \,, $

dabei wird $ \sum_{j=1}^{0}w_j = 0$ gesetzt.
a)
Berechnen Sie die Vektoren $ b_1$, $ b_2$ und $ b_3$.
b)
Zeigen Sie: $ B=\{b_j\; \vert \; j=1,\ldots,3\}$ bildet ein Orthonormalsystem.

Ist $ B$ auch eine Orthonormalbasis von $ \mathbb{R}^4$?

  1. Um diese Formel mit relativ wenig Aufwand zu beherrschen, ist die Beobachtung hilfreich, dass die Summen in der Formel dreimal die gleichen sind. Daher können wir die Formel folgendermaßen umschreiben:

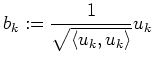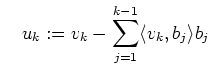    $\displaystyle b_k:=\frac{1}{\sqrt{\langle u_k,u_k\rangle}}u_k$   mit$\displaystyle \quad u_k:= v_k-\sum_{j=1}^{k-1}\langle v_k,b_j\rangle b_j$    

    Damit ergibt sich durch Rechnung: $ u_1=v_1$ und

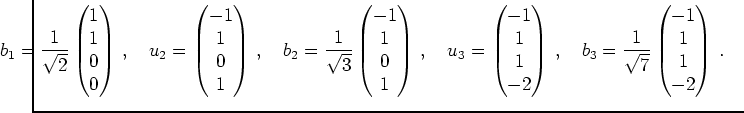
    $\displaystyle \hspace*{-2em} b_1=\frac{1}{\sqrt{2}}\begin{pmatrix}1\\ 1\\ 0\\ 0... ...quad b_3=\frac{1}{\sqrt{7}}\begin{pmatrix}-1\\ 1\\ 1\\ -2\end{pmatrix}\,.\quad $

  2. Durch direktes Nachrechnen kann man zeigen, dass die drei Vektoren $ b_1,b_2,b_3$ jeweils normiert und orthogonal zueinander sind, d.h. ein Orthonormalsystem bilden. Die lineare Unabhängigkeit folgt damit automatisch. Und natürlich bilden die drei Vektoren keine Basis, denn jede Basis im $ \mathbb{R}^4$ muss vier Vektoren enthalten.

    Eine andere Möglichkeit zu zeigen, dass die drei Vektoren ein Orthonormalsystem bilden, ist die Untersuchung der allgemeinen Formeln. Der Schritt von $ u_k$ nach $ b_k$ ist einfach die Normierung des Vektors $ u_k$. Daher sind alle Vektoren nach Abschluss des Verfahrens normiert. Wir müssen also nur noch zeigen, dass sie auch orthogonal sind:

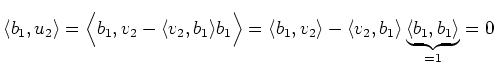    $\displaystyle \langle b_1,u_2\rangle=\Big\langle b_1,v_2-\langle v_2,b_1\rangle... ...,v_2\rangle - \langle v_2,b_1\rangle \underbrace{\langle b_1,b_1\rangle}_{=1}=0$    

    Da $ b_2$ nur ein skalares Vielfaches von $ u_2$ ist, sind auch $ b_1$ und $ b_2$ orthogonal. Die anderen beiden Orthogonalitäten bekommt man mit einer ähnlichen, allerdings etwas komplizierteren Rechnung:

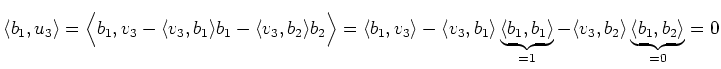    $\displaystyle \langle b_1,u_3\rangle=\Big\langle b_1,v_3-\langle v_3,b_1\rangle... ...\rangle}_{=1}-\langle v_3,b_2\rangle \underbrace{\langle b_1,b_2\rangle}_{=0}=0$    

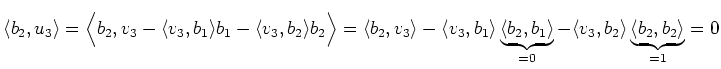    $\displaystyle \langle b_2,u_3\rangle=\Big\langle b_2,v_3-\langle v_3,b_1\rangle... ...\rangle}_{=0}-\langle v_3,b_2\rangle \underbrace{\langle b_2,b_2\rangle}_{=1}=0$    

(Ackermann/Poppitz)
[Zurück zur Aufgabe]
  automatisch erstellt am 19. 12. 2005