Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1180: Untergruppe von GL(4,R)

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Zeigen Sie, dass die Menge

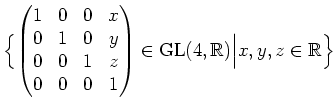
$\displaystyle \Bigl{\{} \left(\begin{matrix} 1 & 0 & 0 & x \\ 0 & 1 & 0 & y \\... ...ht)\in\operatorname{GL}( 4,\mathbb{R}) \Big \vert x,y,z\in\mathbb{R} \Bigr{\}}$

eine Untergruppe von $ \operatorname{GL} (4,\mathbb{R})$ ist.

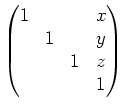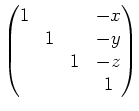Wir wissen, dass die Inverse zu einem Element $ \begin{pmatrix}1 &&& x \\ & 1 && y \\ &&1&z \\ &&&1 \end{pmatrix}$ die Form $ \begin{pmatrix}1 &&& -x \\ & 1 && -y \\ &&1&-z \\ &&&1 \end{pmatrix}$ hat (vgl. beispielsweise Aufgabe 1150). Wir benutzen daher das Untergruppenkriterium um zu zeigen dass wir es mit einer Untergruppe zu tun haben:

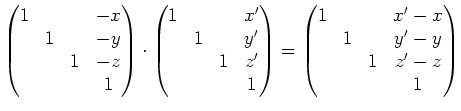$\displaystyle \begin{pmatrix}1 &&& -x \\ & 1 && -y \\ &&1&-z \\ &&&1 \end{pmatr... ...x} = \begin{pmatrix}1 &&& x'-x \\ & 1 && y'-y \\ &&1&z'-z \\ &&&1 \end{pmatrix}$    

Das Produkt $ xy^{-1}$ mit $ x,y$ aus der Menge ist also wieder in der Menge, daher ist die Menge es eine Untergruppe.

(Ackermann/Poppitz)
[Zurück zur Aufgabe]
  automatisch erstellt am 13.  1. 2006