Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1181: Binomialsatz für komplexe Zahlen

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Binomialsatz für komplexe Zahlen
Es seien $ x=a+b\,\mathrm{i}$ und $ y=c+d\,\mathrm{i}$ zwei komplexe Zahlen (mit $ a, b, c, d\in\mathbb{R}$) und $ n\in\mathbb{N}_0$ eine natürliche Zahl. Zeigen Sie mit Hilfe vollständiger Induktion, dass gilt:

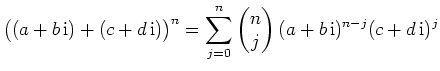
$\displaystyle \big((a+b\,\mathrm{i})+(c+d\,\mathrm{i})\big)^n=\sum_{j=0}^{n}\le... ...{matrix}n\\ j\\ \end{matrix}\right) (a+b\,\mathrm{i})^{n-j}(c+d\,\mathrm{i})^j $

Schreiben Sie diese Formel für $ n=4$ explizit aus. Verwenden Sie dabei für die Binomialkoeffizienten das Pascalsche Dreieck.

Beim Beweis des Binomialsatzes kommt es gar nicht darauf an, ob es sich um reelle oder komplexe Zahlen handelt, sondern nur, dass addiert und multipliziert werden darf und beide Operationen kommutativ und distributiv sind. Daher gilt der Binomialsatz in jedem kommutativen Ring, insbesondere auch über dem Körper $ \mathbb{C}$ der komplexen Zahlen. Es sei an dieser Stelle auf Aufgabe 1117: ,,Pascalsches Dreieck und Binomischer Satz`` verwiesen.

(Ackermann/Poppitz)
[Zurück zur Aufgabe]
  automatisch erstellt am 13.  1. 2006