Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Aufgabensammlung: Lösung zu

Aufgabe 1216: Untersuchung einer Quadrik (konstanter, linearer, quadratischer Anteil, Matrixbeschreibung, Typ, Skizze )

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
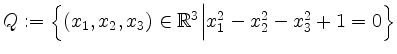Gegeben ist die Quadrik $ Q:=\Big{\{}(x_1,x_2,x_3)\in\mathbb{R}^3 \Big\vert x_1^2-x_2^2-x_3^2+1=0\Big{\}}$ .

  1. Geben Sie den quadratischen, den linearen und den konstanten Teil der Quadrik an.
  2. Geben Sie die Matrixbeschreibung der Quadrik $ Q$ an.
  3. Entscheiden Sie, ob $ Q$ eine kegelige, eine parabolische oder eine Mittelpunktsquadrik ist.
  4. Skizzieren Sie die Quadrik.

  1. Man liest ab: der quadratische Teil ist $ q(x)=x_1^2-x_2^2-x_3^2$, ein linearer Teil ist nicht vorhanden und der konstante Teil ist $ c=1$.
  2. Mit

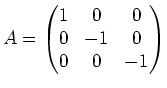
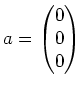
    $ A=\left(\begin{matrix} 1 & 0 & 0 \\ 0 &-1 & 0 \\ 0 & 0 & -1 \end{matrix}\right)$ $ a=\begin{pmatrix}0\\ 0\\ 0 \end{pmatrix}$ $ c=1$

    erhalten wir

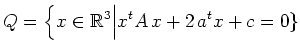
    $\displaystyle Q=\Big{\{}x\in\mathbb{R}^3\Big\vert x^t A\,x + 2\,a^t x + c = 0{\}} $

  3. Wir stellen zuerst die Matrix

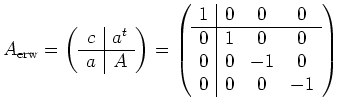
    $\displaystyle A_{\mathrm{erw}}= \left(\begin{array}{c\vert c} c & a^t \\ \hline... ...0 \\ \hline 0& 1 & 0 & 0 \\ 0& 0 &-1 & 0 \\ 0& 0 & 0 &-1 \end{array}\right) $

    auf. Nun ist $ \operatorname{Rang}(A)=3$ und $ \operatorname{Rang}(A_{\mathrm{erw}})=4$, also $ \operatorname{Rang}(A_{\mathrm{erw}})=\operatorname{Rang}(A)+1$. Es ist also eine Mittelpunktsquadrik.
  4. Da $ (-x_j)^2={x_j}^2$ ist die Quadrik symmetrisch bezüglich der Koordinatenebenen.

    Sei nun $ k\in\mathbb{R}$. Schneiden wir die Quadrik mit der Ebene $ x_1=k$, so erhalten wir:

    $\displaystyle 0=k^2-x_2^2-x_3^2+1 \Leftrightarrow x_2^2+x_3^2=k^2+1 $

    also Kreise mit Radius $ \sqrt{k^2+1}$. Das zeigt auch, dass $ Q$ rotationssymmetrisch bezüglich der $ x_1$-Achse ist. Insbesondere haben die Kreise aber immer einen größeren Radius als $ 1$.

    Mit diesem Wissen reicht es dann schon, noch den Schnitt mit der Ebene $ x_3=0$ zu untersuchen, um ein recht gutes Bild von der Quadrik zu erhalten. Es ist nämlich

    $\displaystyle 0=x_1^2-x_2^2+1\Leftrightarrow -x_1^2+x_2^2=1 $

    eine Hyperbel.

    Die Quadrik nennt sich einschaliges Hyperboloid.

\includegraphics[height=\textheight]{quadrik}

(Ackermann/Poppitz)
[Zurück zur Aufgabe]
  automatisch erstellt am 6.  2. 2006